내 소식

오르비

태그

내 태그
입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion
오르비 랭킹
XDK 누적 복권
XDK 경매
RARE

sueal_ [390659] · MS 2011 (수정됨) · 쪽지

2023-08-02 08:07:13
조회수 8,021

예시 문제로 보는 잘못된 기출 공부 방식(23년 6월 14번) - 혹시 이렇게 하고 계신가요?

게시글 주소: https://orbi.kr/00063946610



잘못된 기출 공부 vs. 올바른 공부




안녕하세요


기출 공부를 어떻게 해야할지에 대해 쪽지가 너무 많이 와서


생각나는대로 예시를 보여드리려 합니다




여러분에게 익숙한 문제로 예를 들어볼게요!


2023년 6월 시행 속도가속도 문제입니다.







이 문제를 함께 풀어볼게요


우선 속도 그래프가 4차로 주어져 있습니다


수직선에서 운동방향은 v의 부호가 결정하죠?!


그래서 v가 t축을 뚫고 지나가는 순간이 운동방향을 바꾸는 순간입니다


(추가로 v는 위치 x의 도함수이므로 위치 x의 극점인 순간이 운동방향을 바꾸는 순간으로 해석할 수도 있습니다)




문제에서 운동 방향을 한 번만 바꾸도록 하라고 했으니,


v(t)의 그래프가 그리고 싶어야 하고


v(t) 그래프가 t축을 뚫고 지나가는 순간이 t=0 이후에 한 번만 있어야 합니다!!


즉, 접하는 순간이 많아야 한다고 생각이 들 수 있겠네요




이게 이 문제의 기본적인 틀인데


공부 할 때 여러분의 잘못된 사고 메커니즘과 올바른 사고 메커니즘을 알려드릴게요




빙의 한 번 해보겠습니다




(최악)



아 이거 알아


a=1 일 때 위치 변화량(정적분) 최대임


v(t) = -t(t-1)^2(t-2) 적분하면 답 나옴


~~계산


끝!


아 역시 난 잘해. 풀이랑 답 상황 기억나니까 지루하네, 나 기출은 이제 그만 풀어도 될 듯(ㅎ,,)



=> 대부분 이러십니다




(최악은 아니지만 부족함)



운동 방향을 바꾼다는 표현이 나왔으니 난 뭘 생각해야하지?


-> v(t)의 부호가 바뀌거나, x(t)가 극점을 갖거나였지?


그런데 그게 한 번만 있으려면?





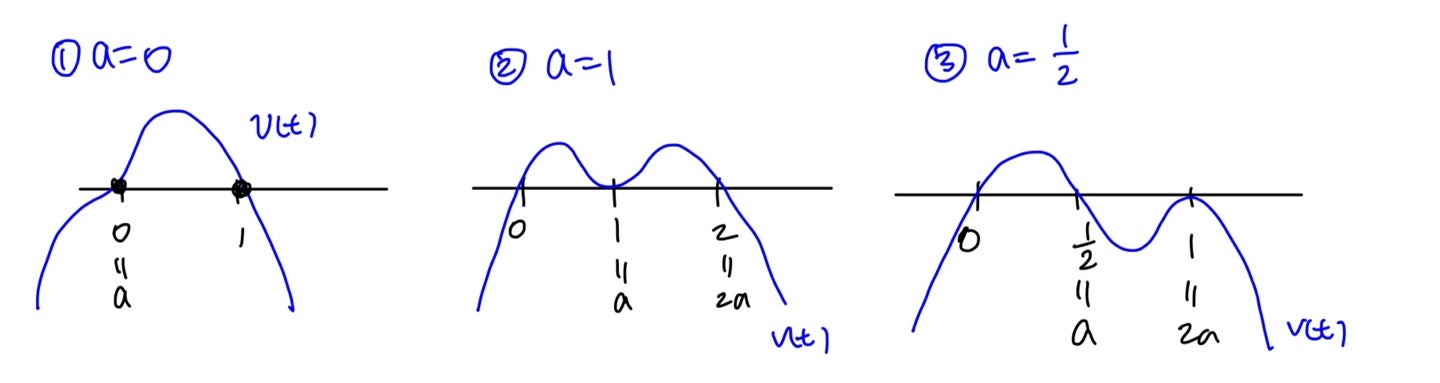
사차함수 v(t)의 그래프가 대충 이렇게 되어야 할 것 같은데?



그런데, 0~2 정적분 값이 최대이려면 다 양수인 가운데 케이스가 유리하겠네?


a=1일 때 최대일 거 같긴 한데.. 일단 구해보자!


~~계산 => 답에 있음


오키 맞겠지 뭐 => 맞음 => 추가 생각 없이 넘어감(그나마 2등급까지 오를 가능성 있음)




(good)




운동 방향을 바꾼다는 표현이 나왔으니 난 뭘 생각해야하지? -> v(t)의 부호가 바뀌거나, x(t)가 극점을 갖거나였지?


그런데 그게 한 번만 있으려면? 사차함수 v(t)의 그래프가 대충 이렇게 되어야 할 것 같은데?




그리고 이건 기출문제들 중 극점을 한 번만 갖을 조건하고도 연관이 있네?


속도 가속도의 형식만 빌렸을 뿐, 사실상 도함수를 활용해 원함수의 개형을 추론하는 문제랑 요구하는 능력이 같구나


평가원이 이걸 자주 강조하네!


그럼 이 세가지 케이스 중 정적분 값 최대는 언제일까?


음.. 양수인 부분만 있을 때가 최대일 것 같기는 한데 혹시 모르니 다 계산해보자


~~(3가지 케이스 모두 계산)


아 역시 양수인 부분이 최대네!




(very good)



(good) 상황처럼 풀었다고 가정


(+)


1. v(t)의 개형에 따라 운동 방향을 바꾸는 횟수가 달라질텐데 이 개형은 a에 따라 달라지겠네?


=> a에 따른 운동 방향 바꾸는 횟수를 새로운 함수 g(a)로 정의할수도 있겠다.



평가원이 이런거 좋아하니까.



한 번 a의 범위(구간)에 따른 g(a)를 생각해보자



=> a에 따른 모든 그래프 케이스 그려보고 케이스별 운동 방향 바뀌는 횟수 몇 번인지 읽어보는 훈련을 함




2. 내가 시험장에서 세 가지 케이스의 정적분을 따로 계산해서 비교해버리면

정답에 확신을 가질수는 있겠지만 너무 시간이 오래 걸리네.



그렇다고 최대일 것 같은 순간이 선택지에 있는데 그걸 찍고 넘어갔다가


다른 상황이 최대여버리면 틀리게되니까 확인을 안하기도 낭패일 것 같고..


조금 더 정적분 값이 최대인 케이스가 언제인지 빠르고 깔끔하게 확인할 방법이 없을까?



=> 고민 + 선생님께 질문해서 케이스별 빼기함수의 정적분으로 이해하면 된다는 것 이해



=> 아! 맞아, 무언가 크기 비교를 할 때는 빼보는 것이 기본 개념이었지!!


교과 개념이 여기서 또 활용되네.



이런 아이디어에 대해 뼈에 새기자! => 진짜 새겨짐



3. 정적분 계산할 때 평행이동해서 더 쉽게 계산하는 것을 배웠었는데 혹시 활용할 수 있는 상황인지 고민해볼까? => 사차 함수 대칭성 활용해 평행이동으로 더 쉽게 계산 => 상황을 보는 눈 길러냈음





(very good) 상황은 제가 재수 할 때 실제로 사용했던 방법입니다.


물론 지금 저의 기준으로 생각했을 때는 그 때의 저도 빈틈이 많았으나(그래도 100점은 계속 나왔습니다)


적어도 저런 방향으로 공부하려고 수학, 과탐 모두 노력했었습니다.




여러분, 기출은 이렇게 공부해야 합니다.


신기하게도 이렇게 공부하면 두 번을 보든 세 번을 보든 같은 문제를 공부하는데도 새로운 관점이 다양하게 보이고 문제가 재해석 되는 경우도 많습니다.



특히 어려운 문제일수록 새로운 관점이 보여서 무기가 많아져요.



이게 다른 풀이를 배우거나 들어봐서 “이런 풀이로도 풀 수 있다”를 아는 것과는 차원이 다릅니다.



나의 실력이 쌓이면서 새로운 시야가 트인 것이거든요.




요즘 기출 공부를 강조하는데, 어떻게 공부해야 하는지 여러분에게 와닿게 설명할 방법이 무엇일까 고민하던 차에 조깅하다가 갑자기 이 문제로 설명하면 좋겠다고 생각이 났네요.


또 생각나면 다른 문제로 적으러 올게요 :)


다들 본인이 위의 네 가지 경우 중 어디에 가까운지 생각해보시고 잘 공부해보시기 바랍니다


 

0 XDK (+1,000)

  1. 1,000

sueal_ [390659]

쪽지 보내기

글쓰기
오르비 1457635번째 회원 되기
아이디 찾기 비밀번호 찾기

오늘의 추천 글

오르비 과외시장

2027 수능 D - 227

오르비 플레이
오르비 RARE
Move
our corporate site
Orbi Class
on-line classes
Orbi Books
educational books & resources
Gae9
humor and fun

© 2000-2026 Move Inc.

orbisoptimus (v17-f0515a)