내 소식

오르비

태그

내 태그
입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion
오르비 랭킹
XDK 누적 복권
XDK 경매
RARE

규토 [319206] · MS 2017 (수정됨) · 쪽지

2022-07-07 00:30:03
조회수 3,689

[규토] 7월 모의고사 해설지 및 총평

게시글 주소: https://orbi.kr/00057465249

(28.2M) [1276]

2022년 고3 7월 모의고사 해설지(made by 규토).pdf




<공통>


13번, 14번,15번, 20번, 21번 난이도가 비슷하게 출제됬고

역시나 22번이 고난도로 출제되었습니다.


22번을 뺀 나머지 문항들은 기출을 열심히 학습했다면

충분히 해결가능했고 다만 시간 안배가 관건이었습니다.

기출문제가 확실히 체화되지 않았다면

쉬4를 제외한 4점부터 턱턱 막혔을 것 같습니다.


22번은 기출뿐만아니라 고난도 N제까지 충분히 체화된

상태에서 접근이 가능한 문제이니

틀렸다고해서 너무 상심하지 않으셨으면 좋겠습니다.

저는 f(x)>=0 일때와 f(x)<0일때로 h(x)를 분할해서 문제를 접근하였습니다.

(손풀이 해설지 참고)


<확통>


무난하게 출제됬고 기출문제에서 크게 벗어나지 않게 출제됬었습니다.

혹시나 무슨말인지 이해를 못해 29번을 틀렸다면

확률밀도함수 관련 개념과 해당 기출문제를 점검해주시기 바랍니다.


<미적분>


27번 부터 당황한 학생이 있었을 것 같습니다.

교육청 해설지에서는 수직보조선을 그어서 처리했지만

손풀이 해설지와 같이 좌표잡아서 푸셔도 좋습니다.


28번은 작년 수능 30번을 약화시킨 문제로

준킬~킬러 학습이 제대로 되어있었다면

시간이 좀 걸릴 뿐이지 충분히 푸실 수 있었을 것 같습니다.


역시나 29번은 계산이 다소 복잡한 삼각함수 도형극한으로

출제되었습니다. f(세타)를 구하는 과정에서

올해 6평 미적분 29번에서 쓰인 각을 구하는 사고가

쓰인 것을 확인하실 수 있었습니다.

긴박한 현장에서는 준킬러 역할을 톡톡히 했을 문제였습니다.


30번은 사설이나 기출에도 굉장히 자주나오는

이차함수 x 지수함수 꼴의 함수를 물어본 문제였습니다.

실수의 개수가 아니라 실수의 합을 물어보았습니다. (실수조심)

x=0에서 극소 or 극대를 갖는다는 발상을 하지 못했다면

현장에서 많이 어려웠을 것 같습니다.


<기하>


26번에서 당황한 학생들이 있었을 것 같습니다.

점p에서의 접선이니 접점의 좌표를 이용한 접선의 방정식이 떠올라야하고

x절편을 주었으니 점 p의 x좌표를 구할 수 있었습니다.

점 P에서 x축에 내린 수선의 발을 H라 하면

삼각형 PHF에서 각변을 c로 표현한뒤 피타고라스의 정리를 쓰면

c를 구할 수 있었고 이어서 k를 구할 수 있었습니다.

3점이지만 4점 역할을 톡톡히 했었다고 봅니다.


28번 선분 FB 연장하는 보조선을 긋지 않았다면

매우 복잡하게 식을 도출해야하는 문제였습니다.

(사실상 시간 제한때문에 못푼다고 봐야함)

문제를 많이 풀어본 학생이라면 선분 OB와 선분 PF'가 서로 평행하지

않을까 의심했을 수 있었을 것 같습니다.

직선 FB가 선분 PF'와 만나는 점을 C라 하면

삼각형 PCF가 이등변삼각형임이 도출되고

삼각형 FCF' 와 FBO가 서로 2 : 1 닮음임을 파악해서 k를 구하는 문제였습니다.


29번 준킬러 역할을 톡톡히 했다고 생각합니다.

조건을 바탕으로 직접 그림을 그려야하는 부분이

난이도를 올려준 것 같습니다.

쪼개서 보면 기출문제에서 크게 벗어나지는 않았던 문제였습니다.


30번 계산도 다소 복잡해서 아마 시간이 없어서 못푼 학생들도 있었을 것 같습니다.

직선 AO와 직선 BC가 서로 수직이라는 조건을 이용해서

점 A에서 선분 BC에 내린 수선의 발을 H라 할 때

BH=x OH=y 라고 두고 문제를 접근하였습니다.

아마 미지수 놓기를 주저한 학생들도 있었을 것 같습니다.

(학생들이 어려워하는 포인트)

평면 PAB와 평면 PAC 사이의 이면각은

이면각의 정의에 기초하여 (교선과 수직인 두 직선이 이루는각)

코사인법칙을 이용하여 구할 수 있었습니다.

실전에서 느꼈을 난이도 역시 높았을 것 같습니다.



<전체 총평>


시험치시느라 고생 많으셨습니다 ㅠㅠ


개인적으로 느낀 선택과목 난이도는 아래와 같습니다.


확통 << 기하 < 미적


예전부터 7월 모의고사는 독고다이 성격이 강한데 (인천교육청)

멋진 문제들도 있었고 좀 너무하다고 느낀 문제들도 있었습니다.

조금 아쉬웠던 건 출제자가 원하는 방향으로 풀지 않으면

식이 굉장히 복잡해는 문제가 많았던 점입니다.

4점 난이도도 전반적으로 다 올라가서

아마 어중간하게 공부한 학생이라면

매우 어려웠을 것이고

기출킬러와 사설 N제 까지 학습한 학생들은

할만한데? 라고 느꼈을 것 같습니다. (극과극)

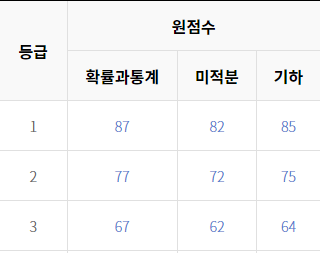
아래 등급컷을 봐도 만만치 않은 시험이었습니다.

이번 시험에서 높은 성적을 받기 위해서는

라이트 N제는 물론 고득점 N제까지 충분히

체화가 된 상태이어야 하니 너무 상심하지 마셨으면 좋겠습니다.


아직 7월입니다 ㅎㅎ

그리고 전범위도 아닙니다.

충분히 역전하실 수 있습니다!

남은 4개월동안 열심히 하셔서

원하시는 바 꼭 이루시길 바랍니다~


화이팅입니다!!


ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ





<규토 라이트 N제 책소개>


규토 라이트 N제 수학1,수학2 책소개 (ver.2023)

게시글 주소: https://orbi.kr/00043536449


규토 라이트 N제 확률과 통계 책소개 (ver.2023)

게시글 주소: https://orbi.kr/00054585618


규토 라이트 N제 미적분 책소개 (ver.2023)

게시글 주소: https://orbi.kr/00054847157


규토 라이트 N제 기하 책소개 (ver.2023)

게시글 주소: https://orbi.kr/00056959272



<규토 고득점 N제 책소개>


규토 고득점 N제 수1+수2, 미적분 책소개 (ver.2023)

게시글 주소: https://orbi.kr/00057259005



미리 짜보는 7월부터 시작하는 반수,군수 커리

게시글 주소: https://orbi.kr/00055284771



<규토 라이트 N제 추천사>


대형학원 멘토진의 수학 교재 리뷰 中

게시글 주소: https://orbi.kr/00042643726


규토N제 풀커리로 수능 미적분 백분위 98% 후기

게시글 주소: https://orbi.kr/00042858563


9월 수학 3등급 -> 수능 수학 1등급

게시글 주소: https://orbi.kr/00034202593


나는 수능에서 처음으로 수학 1등급을 받았다.

게시글 주소: https://orbi.kr/00034215410


수학에 자신이 없었지만 수능 수학 100점!

게시글 주소: https://orbi.kr/00034248098


수포자에서 수능 수학 백분위 92%! (수2 공부법)

게시글 주소: https://orbi.kr/00034690706


저는 평균 7등급이었습니다. 하지만 ?

게시글 주소: https://orbi.kr/00040747823

0 XDK (+0)

  1. 유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.

규토 [319206]

쪽지 보내기

글쓰기
오르비 1447284번째 회원 되기
아이디 찾기 비밀번호 찾기

오늘의 추천 글

오르비 과외시장

2027 수능 D - 291

오르비 플레이
오르비 RARE
Move
our corporate site
Orbi Class
on-line classes
Atom
educational books & resources
Gae9
humor and fun

© 2000-2026 Move Inc.

orbisoptimus (v17-e3325b)