"Chapter. 0 - 함수의 연속"
게시글 주소: https://orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

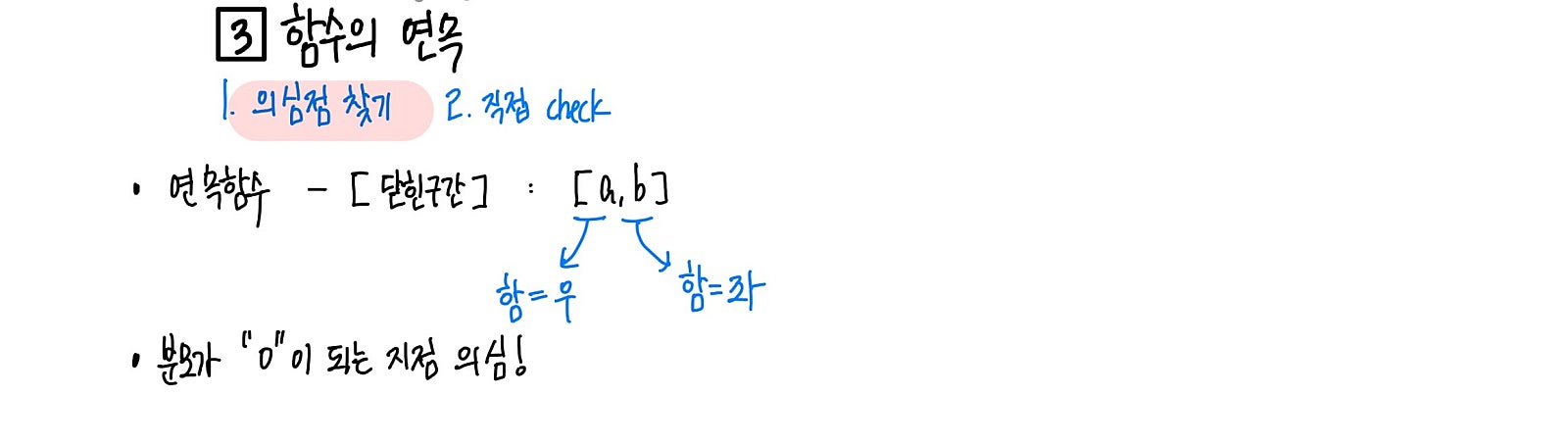
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
그때 재밌었던거 같은데
-
공수처 관할 법원이 중앙지법인데 영장기각당하니까 영장 어떻게든 치려고 우리법...
-
그리운 오르비언 9
ㅅㅅㅎㄷㄹㄱㅅㅅㅅㄹㄱㅍㅎㅇㅈㅇㅍㄴㅌㅅㄹㅅㅌㅇ
-
우리는 언제 창의성과 비판적 사고력을 발휘해야 하는가 0
과거 재미있게 읽었던 책 중에서 하나가 바로 였습니다. 다소 결론이 충격적이었는데,...
-
그런 사람이 누구지...
-
.
-
인가요ㅠㅠ 입덕하고 엄청시끄러운 케이팝 듣기시작하고 국어빼고 다 음악들으면서...
-
연치 경희치 2
가고싶다
-
지금 갈 대학에서도 잘만 하면 대기업 갈 수 있을 건데... 1년 해서 바꾼다고...
-
2주컷 내려하는데
-
의대 N수 1
의대 합격하신 분들 중에서 수능보고 재수하고 1~2년 쉬고 다시 수능 봐서 의대...
-
그리운 오르비언 5
Judge
-
ㅋㅋ.. 15
그냥 진짜 죽고싶을때마다 들으면서 울고나면 좀 낫더라고요 젠장 돈없는것도 죄냐 울고 잠이나 잘래요
-
그립고그리운ㅜ
-
인스타 릴스에서 2
또 방구석 ㅈ문가를 만나버렸는데... TEAM의대가 ㅈ으로 보이지 아주?
-
팜하니의파마늘
-
현우진 풀커리 보단 이해원 쌤 저서들로 공부 해보려는데 시발점 들었으면 한완기를...
-
신발사야하는데 20
뭐사지..
-
미쓰님, 사과맥주님, 중힘님 등등.. 그때 그시절은 평화롭던거같은데 기억이...
-
맞팔구!!! 2
200명 찍고싶습니다~!!!
-
계속머릿속에맴돌아서 요즘 이것만 들음
-
실어증 아세요? 8
시러시러
-
나만 힘들고 나만 불행하고 나만 비운의 주인공이라고 생각한 제 자신이 너무...
-
그거슨 저였고요
-
햄스티링 진짜 터진거처럼 아픔 내일 정형외과 가긴할건더 지금 할거없음..? 엄청...
-
고고
-
메디컬 가스라이팅 좀 있는거같지않냐
-
누군가 관리 해주면 좋겠어
-
어캄
-
아마 귀여운 봇치쨩 이런거 달리겠지?ㅎㅎ
-
아니 언매 미적 지구 개념인강 들어야하는데.. 그럼 인강 듣지말고 독학하란 말임??
-
재수생한테 대가리가 아직 안깨져본 현역입니다... 내신은 2점대에서 2학년 2학기때...
-
대학교 교양의 낭만 끝판왕 인문학 수업
-
깁스하고 휠체어 탄 채로 짝녀한테 가서 인사하면 많이 당황스러워하려나 친하긴함
-
하도 오르비에서 아이고 이러고다녀서 그거 그대로 카톡이나 인스타에서도 사용하는중 ㅋㅋ
-
88에서 69.8로 재탄생했다 모두 축하해줘
-
이런거 하면 재밌겠다 12
댓글 단 사람 프사랑 닉넴 직접 써서 인증해드림 선착 10명
-
할복하실분
-
이거 일도 될까 이거 이도 될까 이거 삼도 될까 이거 오도 될까 ㅈㅅ
-
아쿠아디파르마 오스만투스 꽃향기가 살랑살랑 따뜻한 햇살이 느껴지는 봄에 뿌리기 딱 좋음
-
올해 미적 27 4
난이도 어느정도였나요?
-
ㄹ 11
-
제 지역은 과외 수요가 똥망임요... 과외 학부모님과 연락이 돼도 원하는 금액대가...
-
(들어본적 없음)
-
글씨 인증) 9
악필 인증
-
이렇게 살기 싫은거겠지.
-
내년 의대 증원 1
어떻게 될까요? 충북 원관 울산 불인증 받은데다 다른학교도 말이 인증이지 실제로...
-
살기싫다 15
그냥 이번에 눈 감고 다 해결되면 눈 뜨고 싶다
-
07 현역이고 자이 수1, 수2 하고있습니다. 스블 듣고 싶어서 그러는데 자이랑...












































