문제 푸는 속도가 느리면~ 속도 향상을 위해 문제를 많이 풀어야 한다고 생각하기 쉽습니다. 물론 문제를 많이 푸는 것이 속도 향상에 도움이 될 수도 있습니다. 하지만 무작정 문제 푸는 양만 늘린다면, 고등학교에서 수학을 망칠 수 밖에 없습니다. 왜 그럴까요?

함께 생각해 볼까요? 수학을 공부하는 대부분의 학생들이 문제를 유형화하는 방식으로 양치기를 합니다. 이때, 수학에 재능이 있거나 학습 속도가 빠른 친구들이 현행 과정을 먼저 마치고 선행 및 심화학습을 시작합니다.

문제 푸는 속도가 느리면 선행 및 심화학습을 시작하는 시기도 늦어지는 것이 당연한 결과입니다. 문제 푸는 속도가 빠른 아이들이 더 일찍 공부를 시작해서 더 많이 반복하고 있는데, 문제 푸는 속도가 느린 아이가 "단지 문제 푸는 양을 늘리는 것"으로 따라잡을 수 있을까요? 불가능할뿐 아니라 이와 같이 공부하면 오히려 수학을 망치게 될 가능성이 더 높습니다.

고등학교 수학에서는 중학교 수학에서처럼 누구나 A를 받을 수 있는 것도 아니고, 만약 그렇다고 해도 모두가 상위권 대학에 진학 가능한 것도 아니기 때문입니다. 상위권 대학에 진학하려면 수험생 중에서 상위 10% 안에 들어야 합니다. 모두 똑같이 문제만 많이 푸는 방식으로 공부한다면 학습 속도 상위 10%만 그대로 상위권 대학에 진학하게 될 것입니다.

문제 푸는 속도가 느리다면, 문제푸는 양을 늘릴 것이 아니라 방법을 바꾸어야 합니다. 많이 풀지 않고도 잘할 수 있는 방법으로 공부해야 합니다.

다음 학생의 예를 살펴볼까요?

아래 학생은 기숙형 자사고 2학년(2024년 기준) 학생입니다. 전에는 문제 풀이 위주로 공부했고, 대부분의 문제를 감으로 풀었기 때문에 한 달 전에 배운 것도 기억이 나지 않았다고 하네요. 한 달 전에 배운 것도 기억나지 않는다면, 문제 풀이 위주로 고통스럽게 공부한 선행 및 심화학습이 무슨 의미가 있을까요?

하지만 공부 방법을 바꾸고 나서~ 지금은 겨울 방학 시작(두 달 전)할 때 배웠던 것들도 기억이 난다고 합니다. 전과 다르게 실력이 쌓였기 때문이겠죠? 이와 같이 문제 푸는 양을 줄이고도 실력을 쌓는 것이 가능합니다!

다음 학생(기숙형 자사고 2학년)도 마찬가지입니다. 이제 더 이상 문제 풀이 위주의 대치동 학원에는 가지 않겠다고 합니다. 아래 학생도 공부 방법을 바꾸고 나서~ 전과는 확연히 다르게~ 실력이 쌓이고 있는 것을 느끼고 있기 때문일 것입니다.

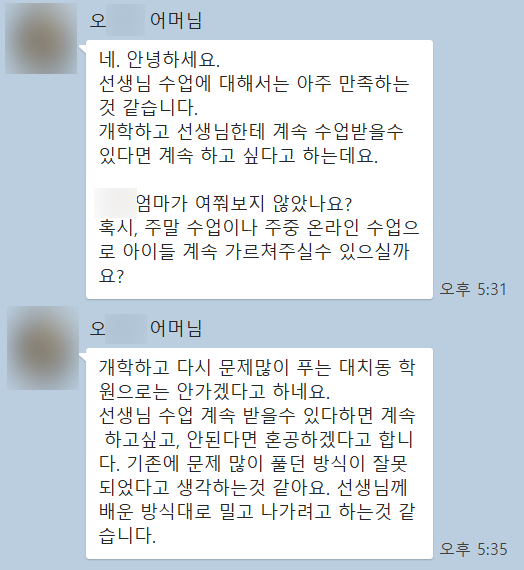
다음은 과천 지역 일반고 2학년 학생입니다. 단지 문제 푸는 양을 늘린 것이 아니라 "생각하는 시간"을 늘렸습니다. 그랬더니 저와 함께 공부한 내용도 아닌데, 1학년 때 풀지 못했던 문제들도 제가 가르쳐준 방식으로 해결할 수 있게 되었다고 합니다! 이와 같이 풀어보지 않은 문제도 풀 수 있도록 공부해야 합니다.

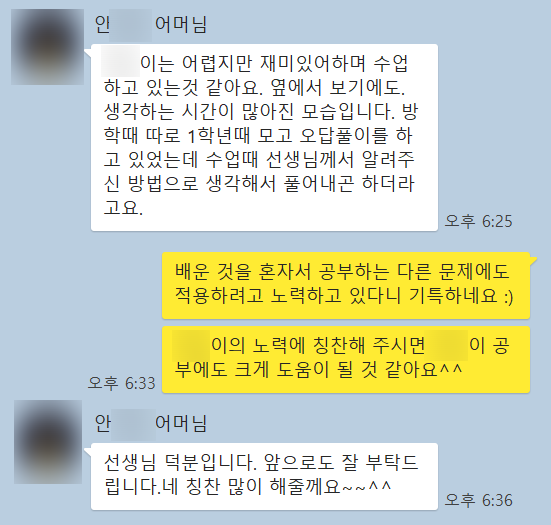
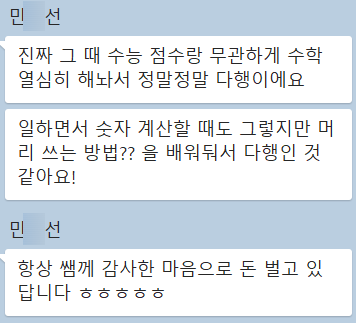
수학을 제대로 공부해두면~ 시험을 잘 보는 데서 그치지 않습니다. 다음은 하나고 졸업생(2014년 졸업, 대기업 직장인)이 제게 보내준 카톡 메시지입니다. 수학을 공부하며 논리적, 분석적 사고능력을 키워 놓은 것이 직장 생활을 하는 데도 크게 도움이 된다고 합니다!