【바보의 수학-문제풀이】 2019 수능 수학 가형 30번 분석
게시글 주소: https://orbi.kr/00032578175
안녕하세요, 입시크릿입니다.
이번 칼럼에서는 2019년에 실시된 2020학년도 수능 수학 가형 (이과) 30번 문제에 대한 ebs풀이와 함께 저의 조금 다른 풀이방법을 제시해보겠습니다.
단순한 해설지는 여러 다른 사이트에서도 충분히 확인할 수 있으므로, 단순한 풀이방법을 넘어 왜 이렇게 문제를 푸는지, 논리적 사고를 하는 방법을 알려드리겠습니다.
저의 이전 '바보의 수학' 칼럼에서 알려드린 수학 공부법을 토대로 하므로 안 읽어보신 분은 한 번 읽고 오시는 것도 도움이 될 것입니다.
(더많은 칼럼과 공부법을 https://blog.naver.com/epsecret 에서 만나보세요)
먼저 30번 문제와 함께 해설지에서 제시한 풀이방법을 살펴보겠습니다.
해당 풀이는 ebsi에 업로드 되어있는 30번 해설지의 일부입니다.
답지를 보지 않고 문제를 푸는 학생도, 답지를 봐도 이해를 하기가 어려운 학생도 있겠지만,
대부분 학생의 경우 "풀이가 이해는 된다. 근데 어떻게 저렇게 똑똑한 생각을 할 수 있는지 모르겠다. 비슷한 문제가 나오면 못풀것 같다." 라는 생각을 합니다.
따라서 과정 하나하나를 분석하며 풀이방법을 생각해내는 근거가 무엇인지, 어떤 방식으로 문제를 풀고 답지를 분석해야 실력이 늘 수 있을지 알려드리겠습니다.
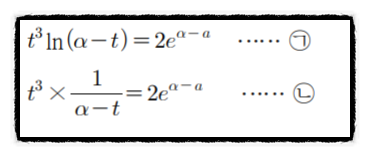
우리가 첫번째로 생각해 내야하는 것은 ㄱ,ㄴ식입니다.
"두 함수가 오직 한점에서 만난다." 라는 것은 미적분에서 매우 많이 쓰이는 성질이죠.
두 함수가 오직 한점에서 만나는 경우에는,
1. 함수값이 같다.
2. 해당 점에서의 미분계수가 같다.
를 통하여 ㄱ,ㄴ을 충분히 유도해 낼 수 있습니다.
이 두가지를 생각해내기가 힘들다면 문제를 풀며 응용력을 기르는 것보다는 그전에 개념공부를 하는 것에 더 비중을 두시는 것이 좋습니다.
이 30번문제의 진짜 어려움은 이 다음에 있다고 생각합니다. 아래 풀이를 읽어보기 전에 먼저 스스로 문제를 풀어보는 것을 추천드립니다.
풀이를 읽으면 이 방법이 모순이 없는 올바른 풀이라는 것은 이해할 수 있지만, 최상위권을 제외하면 답지를 보면서 의문점이 생기는 것이 당연합니다.
1. 저는ㄱ,ㄴ을 구한 다음에 무엇을 해야할지 모르겠던데, 갑자기 ㄱ의 식을 t에 대해서 미분한 이유가 뭔가요?
2. 저라면 ㄱ,ㄴ을 구한 후 두 식을 연립할 것 같습니다. 갑자기 ㄴ도 아니고 ㄱ을 왜 미분할까요?
3. 가만히 있는 3t2을 더 간단한 식도 아니고, 오히려 복잡하게 t3*(3/t) 으로 바꾸는 이유가 뭔가요?
맞습니다. 탁월한 일부 학생을 제외하면 ㄱ을 미분해야겠다는 생각이 잘 들지 않습니다.
저 역시도 마찬가지였으며, 항상 식을 유도한 이후에는 내가 유도해낸 수식이 어떤 성질이 있는지 살펴봐야 합니다.
ㄱ,ㄴ 두식을 보면 우변이 정확히 일치하고, 좌변에 공통적으로 t3이 있습니다.
즉 다음 과정은 2번 질문에서 말씀하신 그대로 공통인수를 최대한 지울 수 있도록 ㄱ,ㄴ을 연립하는게 맞습니다.
마찬가지로 이번에도 식을 변형했으므로 내가 유도해낸 식이 어떤 의미를 가지고 있는지, 특별한 성질이 있는지 다시 한번 살펴봐야 하겠죠?
ln x를 미분하면 1/x 입니다. 즉, 좌변을 미분하면 우변(-t이므로 부호는 바뀝니다)이 됩니다.
이 성질을 이용하면 첫번째 의문점, 왜 ㄱ을 미분하는지 알 수 있습니다.
ln을 미분해도 위 성질에 의하여 다시 문자를 통일시킬 수 있기 때문에, ㄱ식을 미분하면 문자가 통일되어 식이 매우 간단해지는 것이 확실해졌기 때문입니다.
문제에서 준 식만을 바탕으로 바로 ㄱ을 미분하는 것은 쉽지 않습니다.
식을 다양하게 변형해보며 올바른 다음과정이 무엇일지 스스로 생각해 보아야 합니다.
해설지에서는 올바른 풀이를 제시하지만 그것을 생각해내는 방법을 가르쳐주지 않습니다. 그렇기 때문에 단순히 단순히 답지만 봐서는 실력이 늘지 않는 것입니다.
마지막으로 세번째 질문에 대한 답변을 드리면, 저는 출제자가 이미 답을 알고 있기 때문에 이러한 풀이방법을 선택했다고 생각합니다.
저희는 답을 미리 아는 상황이 아니기 때문에, 똑똑한 사람들을 제외하면 바로 풀이처럼 생각하기는 어렵습니다.
위의 제 풀이가 기존 해설지보다 1~2줄 더 복잡할 수 있겠지만, 굳이 답지처럼 변형시키지 않아도 ㄱ을 미분해서 식을 쭉 정리하기만 해도 문제를 해결할 수 있습니다.
반드시 3t2을 t3 x 3/t으로 변형할 필요는 없다는 것이죠.
이렇게 킬러문제로 유명한 수능 수학 30번 문제라 해도 하나씩 하나씩 따지다 보면 크게 어렵지 않게 문제를 풀어낼 수 있습니다.
저의 풀이 방법과 문제 풀이 이론이 여러분께 도움이 되었길 바라며 이만 마치도록 하겠습니다.
감사합니다. :)
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
#07년생#08년생#독학생 오르비의 주인이 될 기회 37 40
-
엄청난이 악질인 이유 0 2
히로인들 이쁘다는 얘기 죽어도 안 함 진짜 딱 한 번 햇음
-
미적 30번을 꼭 봐야할까 1 1
건들 엄두도 안남 ㄹㅇ
-
실모 풀고 딸칠때가 행복햇는데 4 3
하
-
학교가서 신청하면 됨?
-
08) 오늘의 공부인증 4 3
이신혁 모의고사 퓰다가 지쳐서 19 20 포기함설맞이랑 지구 모의고사 오답은 내일...
-
매운해물볶음짜장 시킴 2 2
맛잇겟다
-
사두용미 웹소설 없음? 1 2
요즘 그런게 땡김
-
격자점 3행시 0 1
격하게 흥분되게 하는 새벽 야갤의 글 자세를 고쳐 잡고 조심스럽게 눌러보니 점이...
-
세계관 잘 짜여져 있는 거에서 14 1
카타르시스 잘 느껴지면 회귀수선전 읽으셈 ㅈㄴ 용두용미임 그리고 난 회귀수선전 안...
-
_ 8 1
-
gist 이 사람 3 2
노래 좋네
-
퀄리티 왤케좋지
-
장고랑 악수하고 싶음 1 1
장규진 고양이의 줄임말
-
무난~약불 정도 될 거 같은데
-
빡통 프사 왤케 마니보임 0 1
ㅈㄱㄴ
-
잇올 모고 경쟁률 어떤가요?? 0 0
수강신청처럼 3초컷은 아니겠죠
-
진심 19수능급 핵불 기원합니다 ㅇㅇ
-
오랜만에 맞팔구 3 2
-
아 머야 내 아이민 안 나오네 0 0
구글링으로 나온건 가짜임
-
합성함수항등식 4 0
f(g(x))=h(x)에서 g(x)를 교점의x좌표로 이해하는거 처음봤을때 ㅈㄴ...
-
애초에 어려운 상황이니까 오래 고민한건데 어려운 상황이면 당연히 실수할 확률이 높고...
-
맞팔구 5 1
-
너무 귀여운듯 0 0
너무 귀엽고 멋있음
-
드릴 0 0
드릴 강의보기 귀찮은데 해설지만 봐도 괜찮을까요?? 맞은문제중에서 풀이 비교해보고...
-
내가 먼저 연락하는 경우는 0 2
없을거임 아무래도 그렇다고 봐야지 ㅋ
-
질문받아요 4 0
네
-
2009523 1 2
?
-
tiktok.com/8Wx9CdNm 현재 틱톡에 영상 박제되서 안지워지는중ㅋㅋ
-
연락하지마셈 5 2
내가 먼저 연락하기 전까진
-
질문받음 9 0
제 스펙 앰생남자가슴 큼푸쉬업잘함설대식 398이쁨
-
이거 빨리 읽어보셈 1 0
내신통합사회 내신 통합사회쌤네에 심심해서 통화 4회 하니까 내신통합사회쌤 화 내심
-
느낌이 오고있어 1 0
좋은 예감이 ㅈㅏㄹ 될 것 같아
-
계약학과 분위기 좋음? 0 0
여자. 남자 할꺼없이 다들 사이가 좋나 궁금함
-
길을 잃었다 어딜 가야 할까 0 0
열두개로 갈린 조각난 골목길 어딜 가면 너를 다시 만날까
-
6모접수많이빡셈? 0 0
ㅈㄱㄴ
-
2097152 2 1
가 뭐임
-
소수자로 산다는 것 - 문이과 비율 1:40의 서러움 1 1
제가 졸업한 고등학교는 내신 사탐 선택자 기준으로 문이과 비율이 1:40이었습니다....
-
2315240 0 0
ㄷㄷ
-
2114775 0 0
이거보세여
-
3138914 8 1
네
-
나같은경우는 0 0
이름이 영어임
-
크림진짬뽕 맛있음? 0 1
ㄱ?
-
꼴린다 0 0
사전 찾아봤는데 예시가 "얼굴이 왜 그래? 뭐 꼴리는 일 있어?" 이거네 미친..
-
뭐 먹고 살지 3 0
쌀 먹고 살아야하나
-
나는 먐씨도 만나봄 6 2
진짜 특이한 성인듯
-
암낫큣애니머얼 2 1
uh-uh
-
심리학과 갈까 0 0
나 피파 승부차기 개잘하는거 보면 심리학에 재능있을수도 있는거임
-
비문학 1틀할 때 화작 3틀하는데 나만 이럼?
-
무물보 받습니다 21 0
제 소개 현역 정시 설대 장발돼지 집에 있을 때 선글라스 씀 달리기 빠름
-
무물보 4 0
심심하니 한번 더함
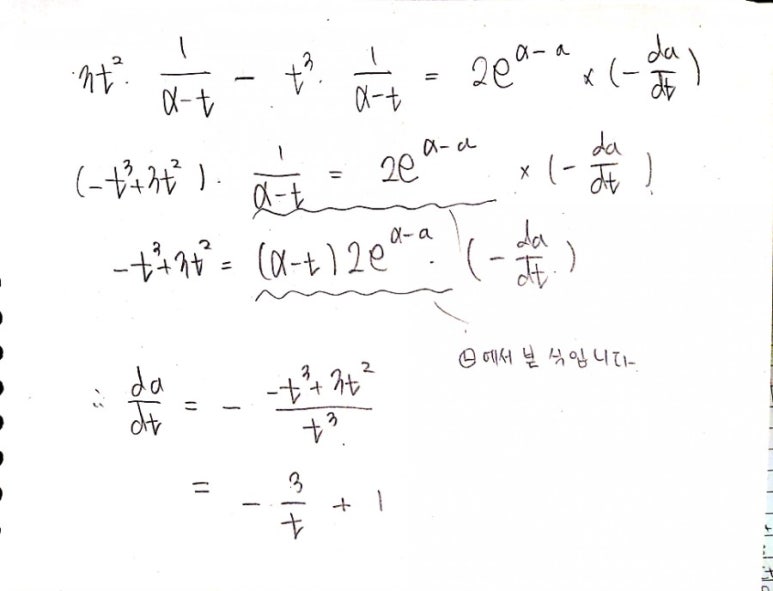
첫번째 댓글의 주인공이 되어보세요.