무브

오르비

아톰

내 태그

내 태그 설정

입시
학습
생활
클럽
직업·취업
Epioptimus
Centurion

오뎅이j [753112] · MS 2017 (수정됨) · 쪽지

2025-06-09 00:56:13
조회수 417

[지구과학1] 6평 19번 문제는 잘못된 문제임 (기하를 모르는 출제자?)

게시글 주소: https://orbi.kr/00073400456

기본적으로 원운동을 하는 행성이라는 것은, "공전 각속도"가 일정하다는 것을 의미합니다.

같은 시간 동안 같은 각도를 공전한다는 것이고 일반적인 외계 행성계 문제에서 전제되어 온 조건입니다.


각속도와 비교되는 개념으로 선속도가 있습니다. 행성의 운동은 기본적으로 3차원상에서의 운동인데, 공전궤도면이 시선 방향과 나란하다는 조건으로 행성의 운동을 2차원상의 운동으로 차원을 낮출 수 있습니다. (z축 성분이 0이니까)

이때 결국 행성의 속도는 2차원 벡터로 표현되는데, 이걸 각 성분별로 분해해서 보는 게 선속도입니다.


쉽게 말해서 행성이 운동하는 게 x축이랑 y축 방향으로 움직이는데, x축 방향만 따졌을 때의 속도와 y축 방향만 따졌을 때의 속도를 선속도라고 합니다. 우리가 아는 시선 속도가 이에 해당합니다.


시선 속도를 y축 성분의 선속도라고 한다면, 90도 꺾인 x축 성분의 선속도도 존재하는데 이를 접선 속도라고 했던 것 같습니다. (엄밀한 용어는 사실 잘 모름...)

그래서 외계 행성의 선속도를 따질 때, 접선 속도는 식 현상이 최대로 일어날 때 가장 빠르다고 할 수 있습니다.


그런데 중요한 사실은, 외계 행성은 중심별을 기준으로 원운동을 하는 것이고, 위에서 말했듯 이는 곧 공전 각속도가 일정하다는 것입니다.

따라서 "접선 속도"는 일정하지 않습니다. 행성의 시선 속도가 최대일 때 접선 속도는 0이 되고, 식 현상이 최대로 일어날 때 접선 속도가 가장 빠른 사인 그래프의 형태를 띕니다. (이는 시선 속도도 마찬가지. 90도 꺾였으니 각변환 공식을 이용하면 접선 속도 그래프는 결국 시선 속도 그래프를 x축 방향으로 평행 이동한 것임을 알 수 있습니다.)

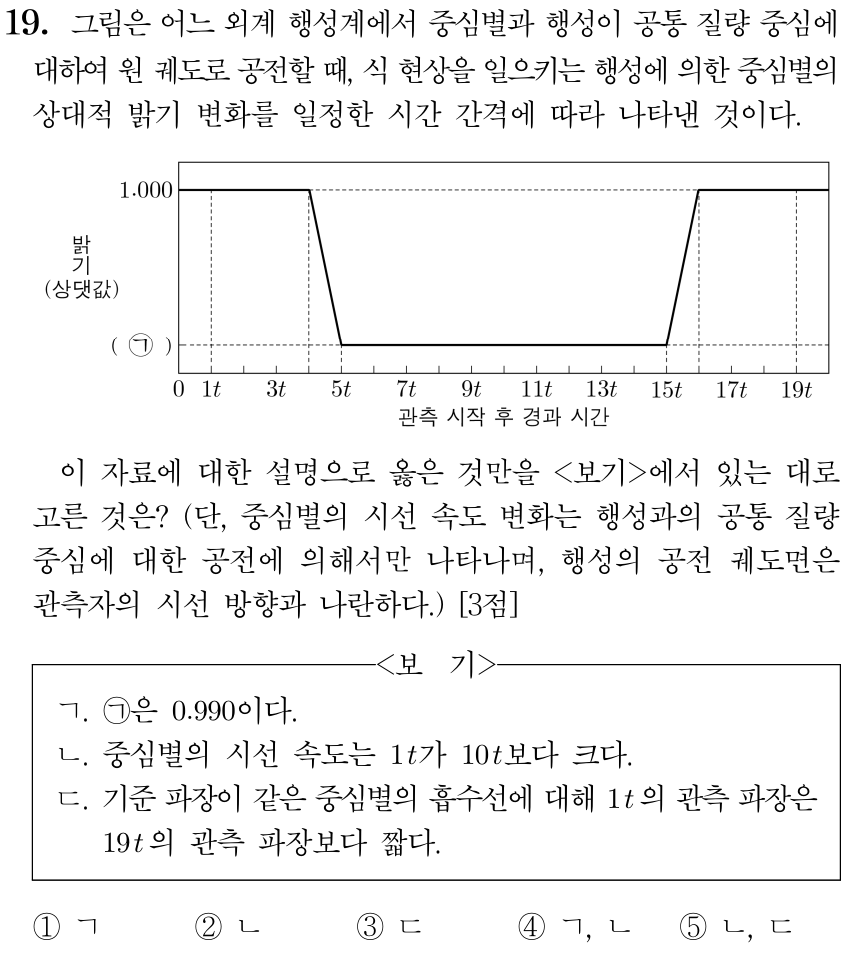
그러면 19번 문제를 봅시다. 19번 문제를 해설할 때 마치 행성이 일정한 속도로 별 앞을 지나간다는 듯이 해설하는 사람이 많습니다. 그러나 위에서 말했듯 "접선 속도"는 일정하지 않습니다.


그러니까, 왼쪽 그림처럼 일정한 시간 간격으로 행성이 저렇게 이동하는 게 아니라 실제로는 오른쪽 그림처럼 일정한 "각도"만큼만 공전한다는 겁니다. 오른쪽 그림 아래를 보면 행성 사이 간격이 다른 걸 볼 수 있을 겁니다.

그렇게 되면요, 사실 이 문제는 굉장히 까다로운 기하 문제가 됩니다. 그래프 조건을 공전 궤도에 나타내면 아래 그림처럼 표현할 수 있습니다.

식현상이 시작되기 직전부터 행성이 항성 안으로 쏙 들어갈 때까지 걸린 시간이 t고, 식현상이 쭉 일어나는 데 걸린 시간이 10t니까 그 기간 동안 행성이 공전한 각도 역시 1:10이겠지요. 이를 세타를 이용해서 표현하였습니다.

R과 r 사이의 관계를 구하는 과정은 R-r과 R+r을 한 변으로 하는 삼각형을 이용해 비교하는 것입니다. 그 과정은 생략하고 결과만 표현하면

로 표현할 수 있습니다. 끔찍하죠? 더 웃긴 건 R과 r 사이의 관계식이 t에 대한 함수라는 것입니다. 그니까, 이 문제는 사실 조건 부족입니다.

그럼에도 불구하고 한번 계산을 해봅시다.. 만약 t가 1°라면, 근삿값을 계산하면 R≈11.0336r가 됩니다.

만약 t가 2°라면, R≈11.14r가 됩니다.

잘못된 해설처럼 마치 선속도(접선 속도)가 일정하다고 하려면? 저 공전 궤도가 식현상이 일어날 때 마치 선처럼 평평해지게 근사하려면 t가 0에 한없이 가까워지면 됩니다. 실제로 t에 0.01°을 대입하면 R≈11.000r이 나옵니다.


웃긴 건, 아무튼 ㉠은 때려죽어도 0.990은 될 수가 없다는 겁니다. t의 값과 상관없이 R은 r의 11배보다 무조건 크니까요ㅋㅋ 혹시 이게 평가원의 숨겨진 의도?


저는 처음에는 '아, 혹시 평가원이 행성의 공전 운동은 그냥 직선 운동으로 가정하고 풀으라는 건가?'라고 생각했는데요, 그러면 ㄴ선지가 말이 안돼요. "시선 속도"라는 표현을 쓴 것 자체가 원운동에서 성분별 속도가 계속 달라진다는 걸 상정하는 건데...


그리고 더 어이없는 건 23수능 20번에서는 원운동 엄밀하게 해석하고 작도도 시켰으면서 갑자기 직선으로 가정?ㅋㅋ 뒤질래?

0 XDK (+0)

  1. 유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.

오뎅이j [753112]

쪽지 보내기

글쓰기
오르비 1397319번째 회원 가입
ddna
1,422,072 건의 게시물이
블록체인에 디지털 공증되었습니다.
901,751
497,321
22,267
574
159

공부를 도와주는 학습자료

2026 수능D - 157

오르비 플레이
오르비 RARE
오르비 과외시장
Move
our corporate site
Orbi Class
on-line classes
Atom
educational books & resources
Gae9
humor and fun

© 2000-2025 Move Inc.

orbisoptimus (v17-e6bd24)