"Chapter. 0 - 함수의 연속"
게시글 주소: https://orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

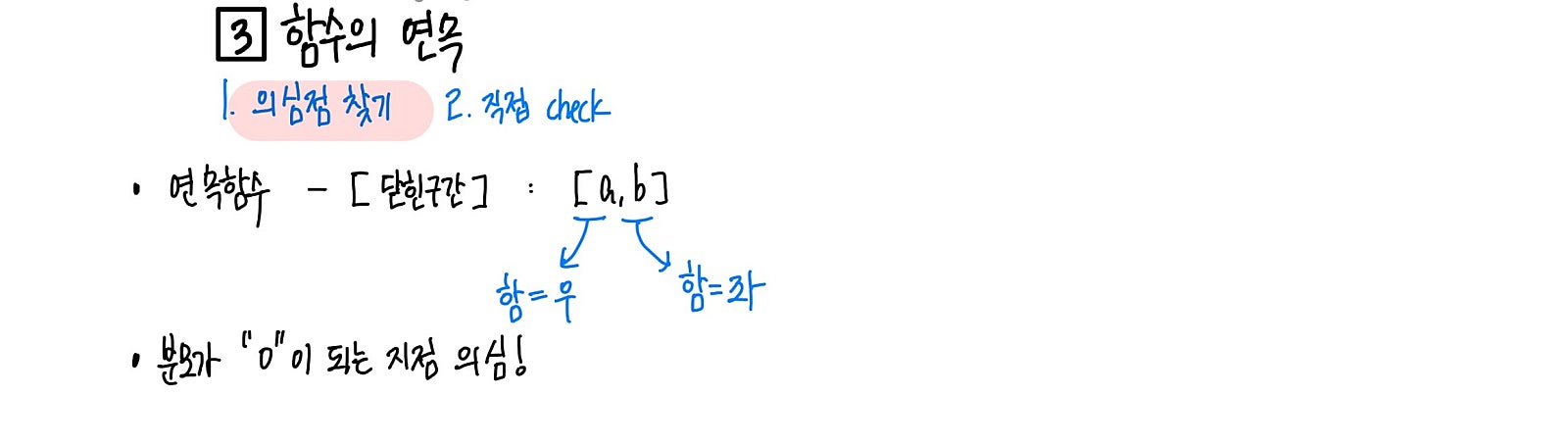
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
어떰 걍 경제 컨텐츠 없어서 퀄 상관없이 필순가 재종 다니지않는 이상 우영호 민준호...
-
내가 국어를 넘 못하나
-
땀이 주룩주룩
-
92근들갑은 ㅋㅋ
-
수특 미적 0
내일 미적분 시험이라 올해 수특 미적좀 보고 들어가려하는데 5~7단원에서 이건 꼭...
-
성님덜,,, 3
현역이도 대학 한번에 가고싶어요 ㅠㅠㅠ 국어는 망했지만 미적 열심히해서 80띄웠단말야 ㅠㅠㅠ
-
처음아닌가 9 수능 기대된다
-
인논 2달차 0
흠…뭔가 감은 잡히는데, 배우는게 많아질수록 생각이 많아지네요. 일단 유형은 모두...
-
그건 학력상승이 아니라 그냥 학력이 높은 사람들이 보는거아님…?
-
마지막 15개정수능 좀 편하게 가자
-
6모 표본 진짜 존나 청정해보이네 일단 05>>06>>>>>07은 맞는듯
-
옯 눈팅하던 시절부터 5년째 보는데 걍 매년 나오는 wwe임 ㄹㅇ 수능가면 결국 입 싹 닫음
-
1컷 50 아닌거부터가 걍
-
현역이 빡 통으로 보이는건 당연한것
-
언확영경사 빨리 내일 성적표 받고싶다
-
요식업 토일 1130-1700 월 50 언저리 사장님이랑 둘이 함 피방 금토일...
-
근데 작년 수학도 1컷 80뜨는거 보고 역대급 빡대갈세대 소리 들어서 2
그냥 수미잡임 특히 수탐은
-
08091011도 빡통일듯.
-
학원에서 내신 기출 책 받았는데 2학기로 되어 있네 ㅋㅋㅋㅋㅋㅋㅋㅋ 화1 내신...
-
XX년생 학력저하설
-
수능때 -정상화-
-
경제 꼭 오셔서 3
제 표점이 되어주십쇼!!
-
07병신설 2
은 11월에 정상화당할 예정입니다
-
아오 이게 만백 100이 안뜬다고
-
경제? 오던가 6
내 위로 올라가보던가
-
82% ~ 88% 사이 표점 같은 집단에 있으면 82%로 나오나요 아님 85%로 나오나요
-
3컷이 왜 24죠...? 이럼 세계사를 안 할 이유가 없어지는데
-
아 에피 못따네 0
탐구 백분위 1씩 내려감
-
내일 80점 이상 나오면 만덕 드림
-
확통런 꿀 빨려면 런 치는 미적러들이 적을수록 유리한거 아님 ?? 사탐런 비해서...
-
ㅁㅊ;;
-
차돌짬뽕 먹을게요
-
신유형 내니까 만표 74에 만분위도 100나오는거 보면 희망 있는것 같은데
-
기하 만표 얼마냐 이럼 10
-
걍.
-
아니 ㅅㅂ 29번!!! (그리고 30번!!)
-
기하하러감
-
어디까지나 일반계고 갔다고 잘났다 ㅈㄹ할 이유가 없음 자사고도 예전에 비하면 폼...
-
싹다 3점짜리만 골라 틀리는 미친짓을 저지르지만 않았어도 1이었네..?
-
흠냐 미적만표 143이네
-
3년전전남친인데 다시 좋아하는거같음 내가 차엿었음
-
66점이면 3턱걸이 가능합니까?????
-
뭐라도 먹어야겠다
-
경제런 마려우신 분들을 위해 작수 경제 만점자가 칼럼 좀 써보겠음 ㅇㅇ
-
부찌 vs 차도루짬뽀옹 11
뭐 먹을까요 첫끼에요
-
앵간하면 그냥 자신 있는 과목 하는 게 맞지 않나 11
물론 과탐은 논외긴 한데 ㅋㅋ 그냥 보다 보면 몇 개월 주기로 계속 여론이 바뀌는...
-
생윤 개꿀이네 2
이난이도에 만백 75..
-
받을꺼노





















































