"Chapter. 0 - 함수의 연속"
게시글 주소: https://orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

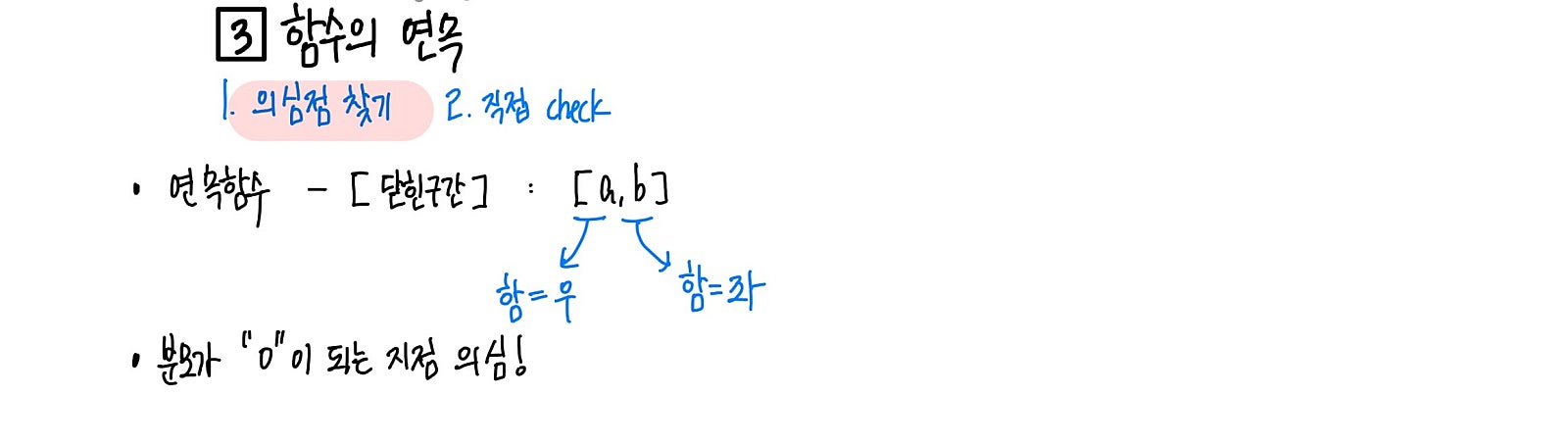
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
올오카 첫강에서 풀고 자신 직시해보라길래 풀어봤더니 공통만 70분 걸려서...
-
진짜임 제가 아까 인스타 맞팔햇다는 분 진짜 개.잘생겻어요 깜짝 놀람 너무...
-
연구소별로 답변까지 어느정도 걸리나요? 채택률은 어떤 편인가요? 전에 올렸던...
-
ㅈㄱㄴ
-
아. 왜 나만 ㅠ
-
이제 슬슬 다들 3
저를 팔로우하시죠 맞팔하겟읍니다
-
짬뽕 마싯겟다 0
이집 존맛탱임
-
1회부터 5회까지 풀었는데 50점은 잘 안나오네요. 계속 44점,45점, 잘보면...
-
ㄷㄷ 좀 불쌍하긴 한데 뭐 어떡해 업보인데
-
국어는 그렇다는 여론이 있는데 수학은 귀납적인 학문이라 좀 다를까요? 시대인재에...
-
오리비콘은 귀여운데 너무하네
-
키미노 운메이노 4
히토와 보쿠쟈나이
-
누구는 헬스 ㅈㄴ 해도 여자들이 관심안주는데 누구는 노력 안해도 여자들한테 인기많음 ㅈㄴ 불공평함
-
세상이 말세구나....
-
일요일 공부 0
N수생들 일요일엔 공부 얼마나 함? 난 그냥 국어 수학 탐구 하나 정도만 하는데
-
중국 매체, '尹 구속' 긴급타전…"한중, 더 가까워질지도" 1
[앵커] 중국 매체들도 윤석열 대통령에 대한 구속영장 발부와 윤 대통령 지지자들의...
-
수학영역 틀딱 기출 활용문제 굳이 풀어야 하나요,,, 요즘은 활용 거의 안나오지...
-
오늘 왤케 잘생기고 예쁜 사람들이 많냐... 30분만 깔짝하고 집 가야겠다...
-
동국대 중도에서 저거 가지고 공부하게 ㅇㅇ 오르비 필통 어디서 삼?
-
제 남자친구가 작성한거에요ㅠㅜ 저는 오르비 들어와서 공부관련 질문들만 올렸었는데...
-
대구한 처음 들었을때 11
대구대학교 한의학과인줄 알았음 근데 학교 이름이 그냥 대구한의대더라
-
으흐흐 3
(음흉)
-
야ㄷ코리아 걔 맞음ㅋㅋ 시청자 차면 시작한댕 https://url1.io/KONnw
-
[동앵과 뉴스터디]“北 지령대로 기밀 수집” 민노총 간첩단 1심 중형 1
윤석열 대통령이 계엄 이후 담화에서 이런 말을 한 적이 있습니다. “거대 야당은...
-
나랑 별 보러 가지 않을래
-
같은 글 자꾸 올려서 죄송합니다 ㅠㅠ 너무 고민돼서,, 금융권 취직을 노릴 예정인데...
-
음란 오르비콘들 6
-
대성 첨 들어가봐서 모르겠어요
-
친친이 쥬지잖아...그런 기초일본어로 날 꼬시려는 음탕빗치들이 너무 많은것같음
-
? ? ? 왜 oriental medical 이 아닌거지
-
책 있으면 추천해주실 수 있나요? 혹시 블로그같은 거… 서론 본론 결론 이런 거보다 좀 더 자세하게
-
…
-
여러분은 둘 다 붙으면 어디 가실?
-
증명이란 공리에서 결론을 도출하는것 공리가 참이면 결론이 참 대우 결론이 거짓이면...
-
야ㄷ코리아 걔 맞음ㅋㅋ 시청자 차면 시작한댕 https://url1.io/KONnw
-
물론 현실에서는 본적없음
-
[속보] 尹 측 "대통령 석방 이유 차고 넘쳐… 증거인멸 염려 없어" 1
윤석열 대통령의 구속영장이 발부된 19일 윤 대통령 측은 "법치가 죽고, 법 양심이...
-
간바레 부엉이짱 5
아자아자 할수 있다
-
이걸내가증명하겟음 근데 안바꿔도못알아보긴함
-
[속보] 尹 옥중 입장문 “평화적 방법으로 의사 표현 해달라” 2
변호인단 발표 윤석열 대통령은 19일 변호인단을 통해 “국민들이 평화적인 방법으로...
-
틱톡이 ㅁ밝힌 서비스 중단 안내 문구 (사진=틱톡)[이데일리 정다슬 기자] 중국의...
-
안녕하세요 저는 고2수학모고 백분위 95~97정도 나오고 고3 14,21번...
-
이걸 학교에 들고다니는애가 있네ㅉㅈ안쪽팔린가?ㅋㅋㅋ
-
다 예비번호 떠서 2월 말까지 기다리게 생겼네... 이럴줄 알았으면 안정 하나...
-
세~노~!
-
현대시 풀다가 해석하는게 너무ㅜ빡쳐서 이럴거면 나도한다 생각하고 써봤어요! 나름...
-
의료법 제2조(의료인) ①이 법에서 “의료인”이란 보건복지부장관의 면허를 받은...
-
그냥 라면 끓여먹을까 흐움
-
국어의 호흡 0
국어 독학서 좋아하는데 국어의 호흡 괜찮나요?
-
생방송 뉴스입니다













































