이진법
게시글 주소: https://orbi.kr/00043396736
이진법.pdf
안녕하세요, 개코입니다.
이 글은 타 커뮤니티에 제가 올린 글을 가져온 것입니다.
이번 주제는 최근 3개년 연속으로 수능에 출제된 '이진법'입니다.
1. 이진법이란?
이진법은 수의 체계입니다. 0과 1만을 이용하여 수를 나타내며, 십진법에서 101=10^2 +1, 110=10^2 +10^1 이듯이 이진법에서는 101=2^2 +1, 110=2^2 +2^1 을 나타냅니다.
구체적인 계산 방식이나 변환 방법은 구글을 찾아보십시오.
2. 이진법의 특징은?
I. 이진법은 수의 체계이다.
이진법은 수의 체계입니다. 이진법은 십진법과 같이 수의 체계입니다. 몇번씩이나 언급하는 이유는 이게 이번 칼럼의 내용의 거의 전부이기 때문입니다.
십진법과 마찬가지로, 이진법으로는 모든 수를 표현할 수 있으며, 하나의 수를 이진법으로 표현하는 방법은 유일합니다.
아무리 낯선 언어라도 한국어와 같이 한 문장에 주어와 서술어가 존재하듯이, 우리에게 익숙하지 않은 수체계인 이진법도 십진법과 같이 하나의 체계입니다.
II. 0과 1만으로 표현된 수이다.
이진법은 모든 수를 0과 1만으로 표현합니다. 이러한 단순성때문에 인간은 이진법을 메모리 장치 등의 여러 방면으로 사용합니다.
또한, 수능 문항을 이진법을 이용하여 출제하여도 수에 대한 감각이 좋다면 이진법에 대한 별다른 이해 없이도 문제를 해결할 수 있고, 체계가 단순하여 이진법에 대한 언급을 피하면서 해설할 수도 있습니다.
이진법 체계가 수능에 자주 출제된 이유는 이것으로 생각됩니다.
3. 이진법과 기출문제
십진법에서, 자연수 n에 대하여 함수
f_d(n)=10n, g_dk(n)=10n+k (k는 9 이하의 자연수입니다.)
라 합시다. 십진법에서 1730은
입니다.
이를 과정으로 설명하면, g_d7(1)=17, g_d3(17)=173, f_d(173)=1730입니다.
오른쪽에서 왼쪽으로 수를 하나씩 붙인다고 생각됩니다.
이와 같이, f_d는 십진법에서 n의 뒤에 0을, g_dk는 n의 뒤에 k를 붙이는 함수입니다.
십진법에서 자연수 n에 대하여 함수
f_b(n)=2n, g_b(n)=2n+1
이라 합시다. 십진법에서 15, 10은 각각


입니다.
한편, 이진법에서 f_b와 g_b는 각각 f_b(n)=10n, g_b(n)=10n+1입니다.
이진법에서 1111, 1010은 각각
입니다.
이와 같이, 이진법에서 f_b는 이진법에서 n의 뒤에 0을, g_b는 n의 뒤에 1을 붙이는 함수입니다.
어떤 자연수는 f_b 또는 g_b를 순서대로 합성한 함수에 1을 넣은 값이며, 이 순서는 자연수와 일대일대응입니다.
이는 이진법이 수의 체계인 것과 상통합니다.
이를 이용하여 아래의 문제를 풀어볼겁니다.
ex) 2020학년도 수능 나형 21번
스포주의) 아래에 풀이가 있습니다.

이 문항의 핵심은 (가)와 (나), 그리고 a_1의 값만으로 수열 a_n이 정의된다는 것입니다. 점화식을 이용하여 모든 n에 대한 수열의 값을 구할 수 있고, 구하는 과정은 모든 n에 대하여 유일합니다.
이는 이진법이 수의 체계인 것과 상통합니다.
평소에 계산할 때 9999=10^4 -1로 생각하여 계산하는 것처럼, 이진법의 감성으로 수가 전개되는 문제에서는 2^n -1 꼴의 수에 주목할 필요가 있습니다. 이 문항에서는 64-1=63이네요.
문항의 풀이입니다.

ex) 2021학년도 수능 가형 21번

이 문항은 위 문항의 변형문제 정도로 생각됩니다. 수열에 대하여 주어진 조건이 점화식임에 주목(->n=1 등의 예외 의심항을 대입)하여 풀면 쉽습니다. 풀이는 첨부파일을 참고해주세요.
아래는 2021학년도 수능특강 수학I 문항입니다.

위의 내용에 대한 이해가 되었다면 아래의 식으로 정의된 수열은 이진법에서 n의 1의 개수임을 쉽게 알 수 있습니다. 100이 2^6+2^5보다 크고 2^7보다 작으므로 조합을 이용하면 답을 쉽게 구할 수 있습니다.(7C2)
다른 내용으로 넘어갑시다.
맨 위에서 설명했듯이, 이진법은 2^n의 꼴로 나타난 수를 더하거나, 더하지 않는 식으로 수를 표현합니다.
9=10-1이고, 1=2-1입니다.
십진법에서 9999에서 10^4를 빼면 -1이고, 99990에서 10^5를 빼면 -10입니다.
같은 맥락으로, 이진법에서 1111에서 10^4를 빼면 -1이고, 11110에서 10^5를 빼면 -10입니다.
이에 대한 증명은 등비수열의 합을 이용하면 쉽습니다.
이를 이용하여 아래의 문제를 풀어봅시다.
ex) 2022학년도 수능 21번
스포주의) 아래에 풀이가 있습니다.

이 문항의 핵심은 (가), (나)를 만족하는 a_n 중에서 (다)를 만족시키는 a_1~a_10은 유일하다는 것입니다. 이진법은 체계이기 때문입니다.
이에 대한 직관이 있으면 문항에 손을 댈 때 확실히 덜 헤맸을 것입니다.
(개인적으로 이러한 문항(유일함이나 함수 관계의 파악이 핵심인 것)이 변별력이 좋다 생각하는데, 비슷한 문항으로는 21학년도 수능 가형 20번이 있습니다.)
나머지는 십진법의 14를 이진법의 1110으로 대하면 정답 상황이 바로 보이게 됩니다. 이진법을 사용하지 않는 풀이는 제 최근 게시글의 22수능 손풀이를 참고해주세요.
문항의 풀이입니다.

철 지난 테마라 생각될 수도 있지만 3년 내내 수능에 출제된 만큼 중요한 테마라 생각됩니다.
그냥 나열만 하면 다 풀리는 거 장황하게 설명하는 이유는 수학 문제 해결에 있어 유일함의 보장은 굉장한 힘이 되기 때문입니다.
어떻게든 문제를 푸는 것이 제일이지만 시험장에서 그 '어떻게든'을 확신하는 근거는 불확실성이 가득한 수능 당일 큰 힘이 됩니다.
이 글은 그러한 근거에 대한 설명 정도로 생각해주시면 되겠습니다. 학습에 도움이 되길 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
용돈은 안받는 대신에 3 0
부모님이 법카를 주심 그걸로 밥 사먹음, 당연히 노는건 내 돈 씀
-
갑자기 궁금한데 0 0
서울대 수리과학부에서 삼슼현 가기 난이도 어떰? 진짜 걍 천외천이라 궁금함
-
ㅇ. 1 0
-
노벨상 받고싶다 0 1
이 나라를 빛내는 사람이 되고싶군아
-
삼촌이름은정진철 0 0
직업은
-
응?
-
피파로 배우는 경제 1 0
피파 잠시 접기 전에 선수 다 팔아서 재화 꽤 남기고 갔는데 공부하다가 오랜만에...
-
문학에서 말하는 긴장감? 8 0
문학 선지에서 나오는 -로 긴장감을 형성한다 이런 선지는 앞부분이 맞는지만 판단하면...
-
안녕하세요 요새 새르비는 6 0
뭐하나요?
-
안 자는 게이있나요? 8 0
나
-
세상이 변하긴변했어
-
일행중에 한명 나보다 운전 잘하는 애 있긴 한데 아직 만 21세 안 됨… 셋이...
-
안녕히 주무시길 5 1
한동안 안 올 생각입니다. 좋은 꿈 꾸십시오.
-
여초커뮤니티 추천좀요 5 0
여자심리공부좀하게여
-
수학 현강vs인강(한탄 글) 2 0
(좀 길어ㅛ요 죄송합니다 ) 단과로 현강다니고 있는데 따라가기 너무 벅차서 인강으로...
-
피파 15카까지 나옴? ㅋㅋ 4 0
갈때까지 갔구나 진작에 탈출하길 잘했다 토티 인강 조지고 접었었는데
-
내일 알반데 4 0
잠이 안오냐.. 망했네
-
님들 수학 문제 값 구하는거에 11 1
루트하고 들어있으면 ㅈ같음? Ex) f(루트3+7)의 값을 구하시오.
-
오늘 점심은 해물짬뽕 5 0
정했음
-
고닉들 물갈이 빨리되는듯 13 1
참 세월이 야속합니다
-
하 자야게ㅛ다... 1 0
오늘은 공부를 구라가 아니라 진짜 안해ㅛ음... 내일은 꼭 열심히 살아야지
-
오빠한테 앵겨 ㅋ 3 1
오빠 믿지? ㅋ
-
벌써 2시 반이네 0 0
할 거 많은데 후
-
나 곧생일이야 8 0
-
진짜진짜 잘게요 5 3
모두 굿밤이에요!!
-
수학 기출 해설강의 0 0
지금 기생집 풀고았는데 강의가 무슨 64강 이렇게 있는데 보통 이걸 다 듣나요?...
-
그만하자 4 1
천박한 메타 불편한 사람들 있음 그만해야지 뇌에 그런 거 밖에 없나
-
좆나 자살하고싶드 2 0
아 씨발또
-
페로로지라 토먼트 시발 5 1
1시간남았다 시발 반짝이 미니언 리트 시발 어휴
-
하 심장 뛰어서 잠도 안온다 9 1
내가 왜 그랬지
-
지랄하지마라 4 1
그냥 하지 마라
-
제2외 해볼까 6 1
-
자야지 2 0
코코넨네
-
약점체크드릴 라노벨 어떰 3 0
어떤데
-
옵치나배그하실분? 0 0
ㅈㄱㄴ
-
존나무섭네
-
내가왜킬러 <- 재밌음 1 0
개그 웹툰으로 추천함
-
하필 남은 그림들이 전대통령이네....
-
세계사나 동사 찍먹하기 좋은 강의나 영상 추천좀 1 0
세계사나 동사로 튀고 싶은데 어떤 느낌인질 잘 모르겠음 평소에 역사 같은거 크게...
-
신하기고 재있미는 사진 1 0
.
-
귀여운 호반우 1 0
-
아니면 새로 사야하나요?
-
저 잘게요 6 4
인지도를 올렸다고 생각하기로 햇어요 그냥 하....
-
미카리님의 말씀을 대신 전합니다 16 4
-
나를 좋아해주는 여자 <<< 어딘가 정신 나가있는 것이 분명
-
뭐 제가 그런 경솔한 글을 쓴것도 잘못이지만.... 14 2
그 댓글에도 약간 문제가 있지 않았나.... 생각해요 전 그냥 가볍게 농담이나 하려는 거였어요
-
무물보 12 0
ㅋ
-
오노추 3 0
-
얘는 왜 가입하자마자 산화됨? 12 3
알칼리금속인가


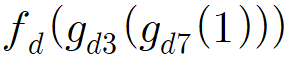

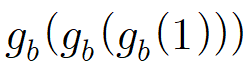
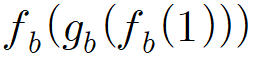


































호형훈제 ㄷ ㄷ이분 모밴임?