표본표준편차에 관한 질문

Question

미적분과 통계기본 개념서들에 보면'모평균의 추정과 신뢰도' 파트에서모집단의 분포가 정규분포를 따를때 모평균 m은 다음 범위에 있다.(X는 표본평균, n은 표본의 크기 , 델타는  표준편차)95%의 신뢰도로서 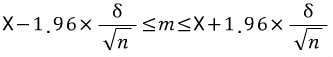 *그리고 실제로 모집단의 표준편차 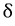 를 모르는 경우가 대부분이다. 이때 표본표준편차를 이용해도 위의 신뢰도는 성립한다.그런데 제가 궁금한건 모집단의 표준편차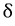 를 모른다고 표본표준편차를 위의 식에 넣어도 성립한다는 건데표본표준편차란 대체 무엇이죠??? 표본평균의 표준편차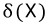 와는 다른건가요???  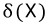= 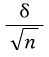라고 알고 잇는데 이걸 대입하라는 소리는 당연히 아니겠죠?;;;; 설명좀부탁드립니다. ㅠㅠㅠㅠㅠ

☞하라남편☜ · Accepted Answer

뭘 궁금해하시는지 대략 알 것 같아서 내용은 제대로 안 읽었습니다만, 해결이 될 겁니다.

'표본표준편차'와 '표본평균의 표준편차'는 당연히 서로 다릅니다.
예를 들어서, 한국에 있는 고3 학생들의 키를 생각합시다. 몇 십만 명 될까요? (모)평균은 170이라 치구요.
'표본평균'은, 여기서 100명의 학생을 임의로 뽑았는데, 그 학생들의 평균키입니다. 중요한 건, 그냥 '표본평균'은 '변수'입니다. 정해진 수가 아니란 말이죠. 즉, 서울에서 100명을 한 번 뽑아 평균 내는거랑, 부산에서 100명을 한 번 뽑아 평균 내면 차이가 있겠죠? 170에 근접할 거라는 건 예상할 수 있습니다. 우연히 좀 큰 놈들만 뽑으면 175가 나올 수도 있겠지요.
'표본평균의 평균'은, 방금 말한 변수 표본평균들의 평균입니다. 즉, 서울에서 100명 뽑고 부산 100명 대구 100명 여러 동네에서 100명 씩 뽑으면 변수가 여러 개 있죠? 그것들의 평균입니다. 서울 애들의 평균 169 부산은 평균 170 대구는 171, 대충 170 근처에서 형성되겠죠? 그래서 표본평균의 평균은 모평균과 같습니다.(정확히 왜 같은 지는 책에 증명이 있는지는 모르겠는데, 직관적으로 받아들일 수 있겠죠?)
'표본평균의 표준편차'는, 말 그대로인데, 표본평균은 100명의 평균이니까, 모평균에 근접할 겁니다. 전국의 어느 지역에서든 100명을 뽑아 키를 평균내면(표본평균) 진짜 특이한 동네를 제외하고는 그 평균이 170에 근접하지 않겠어요? 그러므로 170에서 흩어진 정도가 작으니까 표준편차는 작을 수 밖에요. 그걸 루트n으로 나눠줬다고 생각하시면 됩니다.

모평균을 추정할 땐 100명 씩 여러 번 뽑을 필요 없이, 서울 애들 100명 한 번만 뽑아서 모평균을 추정합니다. 여러 번 뽑으면 귀찮잖아요. 통계조사하는 이유도 없구요. 서울의 학생들이 가장 표준적이라 생각해서, 서울 애들 100명 뽑아 키를 측정합니다. 이 애들의 평균은 위에서 말한 '표본평균'인데, 이 100명 간에도 표준편차가 있을 겁니다. 이것이 '표본표준편차'이구요. 이건 전국 모든 학생들의 표준편차(모표준편차)와 같습니다. 전국 학생들의 키의 분포가 155~165에 30%, 165~175에 40%, 175~,185에 30%라고 칩시다. 임의로 뽑은 서울 애들의 키는 위의 분포와 비슷하겠죠? 물론 100% 같다고 할 순 없지만, 거기에 근접할 거라는 건 생각할 수 있죠. 그래서 모표준편차 자리에 집어넣어도 되는 겁니다.


말재주가 없어서 간단한 내용을 너무 어렵게 말한 게 아닌가 걱정되네요. 궁금하시면 다시 물어보세요~

표본표준편차에 관한 질문

최근 게시글 · 더보기

공부를 도와주는 학습자료