Art149 - 수학 22번 여러 풀이와, 그 선택의 이유 정리

문제를 읽고 구하는 것이 무엇인지를 확인합니다.

=결과에서 출발하여 풀이설계를 합니다.

=> 아는 것과 연결-연결

보라색을 보고, k값을 직접 구하는 게 아니네~ 

저 꼴 통째로 구해야겠다. 이렇게 추측할 수 있습니다.

크게 4가지 조건들이 있는데, 해석하기 쉬운 조건부터 해석하시면 됩니다.

풀이설계를 해보니, 대략 문제는 저런 순서로 이루어질 것 같죠?

1=>3=>4

3번은 일단 A가 구해져야 쓸 수 있으니까요.

저는 1,2,4번 조건이 일단 제일 정리하기 쉬우니

1,2,4번조건에 먼저 접근했습니다.

직선이 곡선과 만나는 3번조건은 바로 접근하기 어려우니까요.

뒤에서 접근하는 4번, 앞에서 접근하는 1번은 바로 진행가능합니다.

2번은 간단한 조건이라 언제든 써먹을 수 있을 것 같구요.

풀이순서는 꼭 이렇게 해야 되는 것이 아닙니다만,

이런식으로 

왜 이런순서로 봐야 하는지, 본인 나름의 논리가 있어야 합니다.

단순히 해설을 이해하는 것과, 

조건하나하나 왜 이런 순서로 봐야하는지 정리하는 것은 정말 다른 문제입니다.

그냥 이게 해석하기 쉬울 것 같아서요. 이런 이유라도 괜찮으니

그냥 아무생각없이 해설을 감상하고 끝내지 마세요~

여튼 

1번 조건부터 확인해볼게요.

일단 풀 수 없는 방정식이니까, 정리정도만 할 수 있겠죠?

참고 : 1번조건 정리 이미 할 수 있다면 

여기 부분은 가볍게 대충 읽으셔도 됩니다.

A의 x좌표를 a로 두고 정리를 해줬습니다.

이 때, 치환은 선택입니다. 

굳이 안 해도 되는데, 저는 좀 더 잘 정리된 걸 잘 보려고 치환했었어요.

그럼 A좌표를 a를 이용해서 (a,2^(a+1)) 로 나타낼 수 있게 됩니다.

그리고 , 보라색을 이용해서

내가 구하는 것을 a+1 + 2^(a+1) 로 바꿔줬습니다.

왜? 아는 것과 아는 것을 연결-연결

x좌표를 a로 안 두고 , 푸는 풀이도 있는데 상관없습니다.

본인이 하던대로 , 배운대로 하시면 됩니다.

어차피 근본은 똑같아요.

이번 글에서는 a를 도입한 풀이 위주로 설명드릴게요.

다음으로 4번조건을 이렇게 해석했습니다.

넓이16 = 1/2 X 밑변 X 높이

밑변 : 선분AB

높이 : 원점과 AB사이 거리

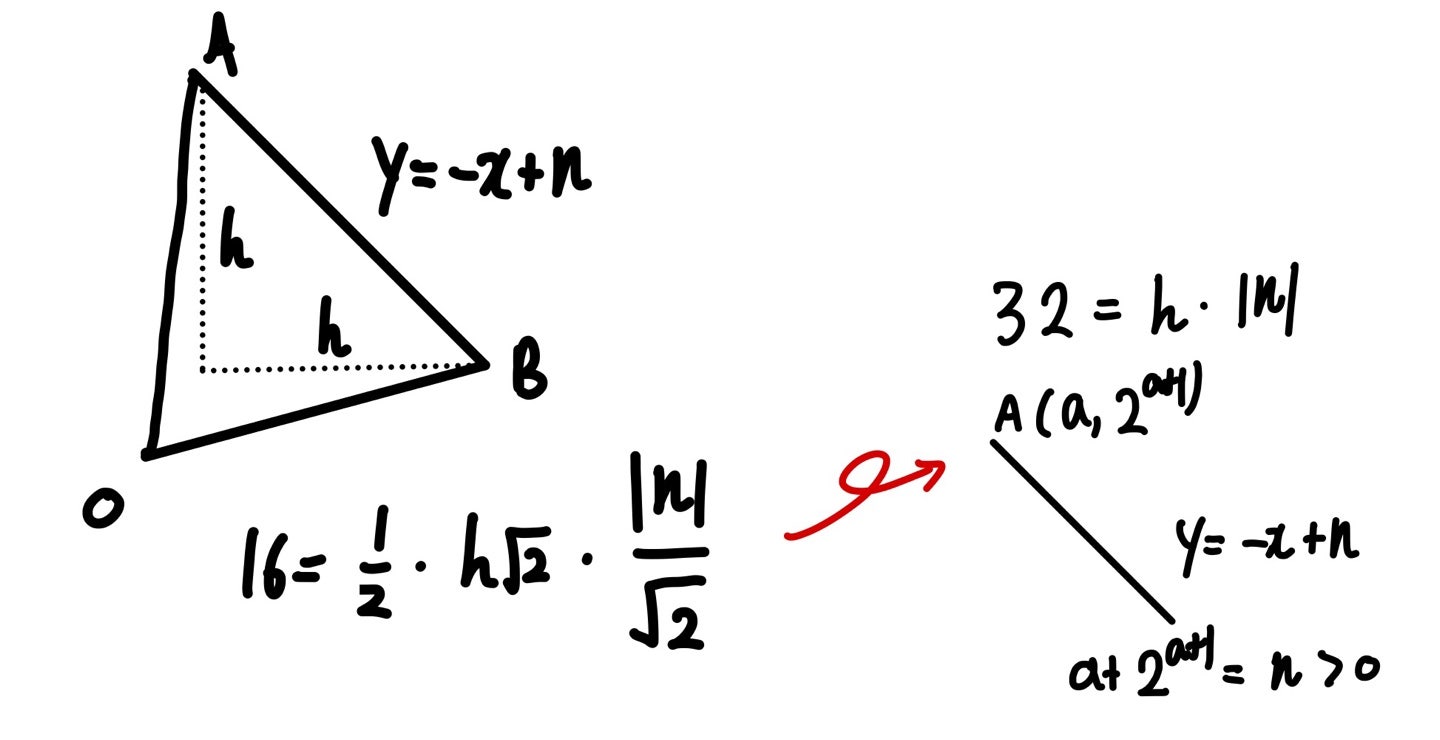
점과 직선사이 거리 공식을 쓰기 위해 y=-x+n 

이렇게 n이라는 미지수를 도입했고,

AB를 구하기 위해, h라는 미지수를 도입했습니다.

(기울기 => 직각삼각형 작도)

A가 y=-x+n의 점이므로, n은 A의 x좌표,y좌표를 더한 값이고

내가 구해야 되는 꼴과 매우 유사하니까 이젠 목표가 n을 구하는 걸로 바뀌었죠.

이것도 내가 아는 것과 아는 것 연결-연결

그럼 이제 h만 구하면 답을 구할 수 있다는 것을 알 수 있고,

이건 3번 해석을 해서 h를 구해야겠다~ 라는 생각을 하고 

3번을 바라볼게요.

풀이는 크게 평행이동을 하는 풀이 / 아닌 풀이로 나뉘는데 

저는 둘 다 할 수 있어야 된다고 생각해요.

내가 논리적으로 납득할 수 있는 풀이, 

내가 시험장에서 이렇게 생각할 수도 있었겠네?

이런 풀이들은 다 가져가보세요.

평행이동 풀이부터 먼저 해볼게요.

대부분의 강사분들이 해설하는 방법인 A가 2^(x+1) 위의 점이다. 이걸로 푸는 풀이입니다.

이걸 그냥 그렇군~~ 하고 넘어가면 절대 안 되고, 

내가 왜 이 곡선을 생각해야 되는지 생각해보셔야 됩니다.

생각의 흐름은 

평행이동인가? => 관찰하려면 A를 밑이 2인 지수함수위로 올려야 된다 => 2^(x+1) 도입

실전에서 이런생각을 못했더라도, 

아 평행이동을 관찰하기 위해서, 밑이 같은 그래프를 그리는 거구나~

이런식으로 아이디어를 가져가야지, 이건 너무 발상적이야. 라던가

내 머리로는 이런거 못 떠올릴 것 같아.. 이렇게 넘어가면 안 됩니다.

다음으로, A를 지나는 새로운 곡선을 도입하지 않고,

그냥 점 A와, B를 지나는 곡선을 관찰하는 평행이동 풀이가 있습니다.

먼저  

저게 그냥 h=3인가? 이것도 그렇게 부자연스럽지는 않아요.

왜냐면, h를 구해야 되는데 특수한 값들부터 생각하는 건 당연하고,

점 A와, B가 지나는 곡선 꼴을 비교해보면  -3이 거슬리거든요.

그래서 일단 3인가? 하고 넣어서 확인해보면 h=3 맞네~ 하고 답 내면 됩니다.

+ 

a+1 / x-2 => 3칸차이? 맞나? 하고 h=3을 넣는 것도 마찬가지입니다.

일단 관찰을 위해, 특수한 숫자를 넣어보고 관찰하는거죠.

이것도 당연하게 해왔던 사고입니다.

여기까지는 완전 직관풀이라면

이 직관에 논리적으로 살을 더 붙여볼게요. 

원본곡선인 2^x 기준으로 생각해보는겁니다.

y좌표가

A : 원본기준 2배

B : 원본기준 1/4배 / -3

배율보정 8배 => 보정하려면 x방향 +3칸차이

-3 =>기울기 -1인 직선에서는 => x방향 +3칸차이

+3으로 겹치네. 

요렇게 좀 더 직관적이면서도 논리적으로 관찰할 수 있습니다.

숫자가 우연히 같아진 게 아니라, h는 하나의 값으로 나와야 되기 때문에,

문제 데이터 => h=3을 만들도록 설계돼 있습니다.

아마 직관적으로 3인가?? 이렇게 생각하신 분은 

아마 대부분 비슷하게 이런생각을 의식적으로든 무의식적으로든 했을 것 같아요.

우리가 그래프 추론 문제에서 특수한 케이스부터 검증하는 것 처럼,

직관은 강력한 무기입니다. 다만, 직관 후 검증이 꼭 필요합니다 

다음으로는 평행이동 관점을 생각 못 했을 때의 풀이입니다.

h를 구해내기 위해 아래처럼 식을 세팅합니다.

이 때, 풀어낼 수 없는 초월방정식을 

왜 정리하는지에 대한 이유를 알고 있어야 합니다.

나의 타겟은 h고, 

h는 무조건 이 조건에서 나올 수 밖에 없다는 걸 알고 있기 때문에 

정리하면 =>h 나올거야~~ 라는 생각을 가지고 접근을 하는 거죠.

그냥 아몰라!! 일단 식으로 풀자. 이거랑, 

h는 이 조건을 해석 했을 때 나오는 걸로 정해져 있으니까,

h에 포커스를 맞춰서 식을 정리하자. 이건 다른 태도입니다.

기울기 -1 => 직각삼각형 소환

A기준으로 +h,-h 만큼 이동한 점이 B인데

그 점이 2^(x-2)-3 을 지나니까 대입해서 식을 뽑아내고 식을 정리합니다.

여기서 h=3을 구하는 3가지 방법을 간단하게 적어볼게요

-------------------------------------------------------------------

첫번째는

그래프를 그려푸는 풀이입니다. 

2^(a+1)은 양수인 상수.

h-3=t로 편의상 치환했는데, 치환 안 해도 그래프는 쉽게 그릴 수 있어요.

------------------------------------------------------------------------------------

2번째 방법은 부호로 접근하는 풀이입니다.

이렇게 미지수가 , 식보다 많은 경우

정의역/부호/홀짝/자연수정수 같은 조건을 관찰해서, 

풀이의 방향을 좁힐 수 있습니다. 미리 안 되는 거 필터링하는거죠.

요게 부호를 보는 당위성이라고 생각하시면 됩니다.

----------------------------------------------------------------

h-3이 공통으로 보이니까 막 나눠서

기울기로 해석하고 싶을 수도 있잖아요?

h=3이 아니라면, 

2^(a+1) : 양수

빨간점선박스 : 2^x 위 두 점 사이 기울기 => 양수

근데 곱해서 -1 => 모순

이렇게 h=3을 뽑아낼 수도 있어요.

+ 그냥 B의 좌표를 미지수로 잡고 계산하셔도 당연히 동일한 결과가 나옵니다.

이때, 계산을 편하게 할 수 있게, 적당히 좌표를 조정할 수 있습니다.

B(4b,~) 이런식으로. 내가 왜 4b로 설정했는지 설명할 수 있으면 됩니다.

+ 오늘 처음 본 풀이인데, y=-x+n이라는 직선을 점 A,B 둘 다 지나니까

x좌표+y좌표 합이 동일하다는 식을 뽑아낼 수 있고

=>계산을 편하게 할 수 있게 적당히 B의 좌표세팅하고 계산해서

=>둘의 좌표차가 3인 걸 알 수도 있습니다. 

--------------------------------------------------------------

사실 제일 중요한 건,

평행이동으로 풀었냐~ 식으로 풀었냐~가 아니라

왜 이렇게 풀었느냐 입니다.

왜 그렇게 풀었어요? 했을 때 답할 수 있어야 합니다.

잘 아시겠지만, 해설을 이해하는 것과

실전에서 문제를 풀어나가는 건 매우매우 차이가 큽니다.

정말정말 열심히 칼럼 썼습니다ㅎㅎ

좋아요 댓글은 큰 힘이 됩니다. 감사합니다.