[에라둔] 역학 문항에서의 미래와 과거
게시글 주소: https://orbi.kr/00069303116
계산적으로 중요한 내용들은 아니고 그냥 편히 읽으시면 될법한 내용들입니다.
역학 문항을 풀다 보면 여러가지 상황을 마주하게 되는데
종종 동일한 카테고리를 마주하게 됩니다.
이번에 다룰 내용은 어찌보면은 상대속도와 조금 관련이 있을 수 있습니다만 일단 접어두고.
아래 문항들의 공통점이 무엇일까요?

20230618


20210911


20130920
세 문항의 공통점은 두 물체가 모든 지점에 대하여 운동 방향, 속력 모든것이 동일한 상황들입니다.
이전에 저도 문항 출제를 할 때 위와 같은 상황을 이용하여 문항 출제롤 하곤 했는데
위와 같은 문항을 출제하면 참 좋은게 v-t그래프를 옆으로만 삭 밀어주면 되기 때문에
검토하기가 수월해서 즐겨냈었던 기억이 어렴풋이 납니다.
거두절미하고
어떻게 보면 위와 같은 문항들은 상대속도를 활용할만한 문항들 중에서도 특수한 케이스라고 생각을 하는데
저같은 경우에는 두 물체에 대하여 가상의 시간차 t를 가정하고 문제 풀이를 하는것을 선호합니다.
뿐만 아니라, 시간차 t가 난다고 생각하고 문항을 바라보면 좀더 문제 상황을 직관적으로 파악하기도 좋지요.


예를 들어 위 문항의 경우엔 B의 2초 뒤 모습이 A라고 생각하면서 풀면 문제 풀이가 아마 수월하겠죠.
일단 ㄱ이 바로 나올것이며
2초뒤 B가 정지할테니 평균속력 2라는 점에서 v=4가 바로 나올것이며
dv=4인동안의 시간이 2초니 가속도가 2인것도 술술 나올것입니다.


20210911
마찬가지로 위 문항도 B가 t초뒤의 A모습이라고 가정한다면 3vt=L이 나올것이며
우리는 자연스레 A가 p에서 q까지 이동하는데 걸리는 시간이 t라고 할것이기에
평균 속력 공식을 이용하여 1.5vt=0.5L과 같이 문항들이 순둥순둥하게 풀릴것입니다.
위와같이 동일한 경로, 운동 상황을 공유하는 문항의 경우에는 결국엔 대부분 문항에서 요구하는것은
두 상황에 대한 연립일것이며, 이 연립과정이 가감의 과정이기 떄문에
사실 t로 두고 문항을 풀면 쉽게 풀리는 경우가 많습니다.


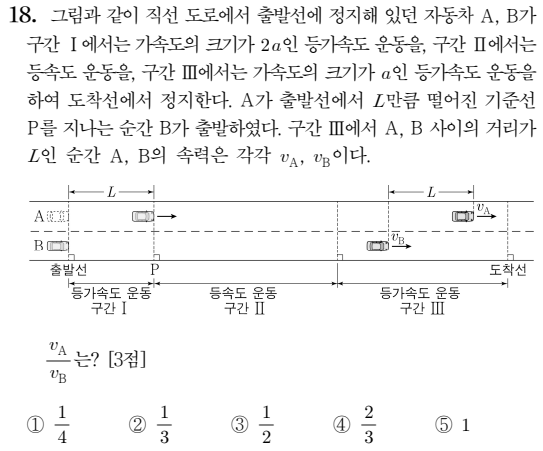
20230618
위 문항의 경우에도 마찬가지로 역시 B의 t후 모습이 A라 생각하고 풀면 풀기가 수월할것입니다.
등가속도 운동 구간 I에서의 가속도를 2a라 하면 (0+2at)t/2=att=L이 나올것이며
이후 vb인 B가 시간 t 후 속력이 va가 된다고 하면 자연스레 (va+vb)/2 * t = L이 나오게 될것입니다.
그리고 구간 3에서 시간 t동안 속력이 변하였는데 이것이 va-vb일지 vb-va일지는 잘 모르겠습니다.
사실 시간 t라는 차이를 생각해보면 B가 출발할 때 이미 가속된 A가 있기에 거리차가 L보다 벌어질텐데
다시 L로 감소했다는 포인트를 보면 아마 가속도가 감소했음을 알기 수월하겠지요.
그러한 이유로 (va+vb)=2L/t, (vb-va)=at=L/t
va+vb : vb-va = 2:1, 2vb-2va = va+vb, 3va=vb, va:vb=1:3 이 나오게 될것입니다.
저같은 경우에는 두 물체가 동일한 경로를 운동하면 습관적으로 동일한 운동까지 하는지를 체크합니다.
아마 위와같은 유형들을 깔끔하게 푸시는 분들이라면 위의 개념을 숙지한 상태에서
그 이상은 본인의 직관, 암산 등으로 인한 최적화 정도의 차이만이 존재할것입니다.
만약, 위와 같은 수식적 풀이가 다소 어렵다면 그냥 모든 시간 영역을 t미지수로 두고 풀어보시거나
vt 그래프를 정성스럽게 그려보시는것을 권장드립니다.
아마 그래프를 그리시다 보면 자연스레 평행사변형과 친해지게 될겁니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
직장인 존경함 2
지금 알바 하는 분이 도망가서 주5일 알바 홀서빙 3주찬데 너무 힘듦 손님이 많은...
-
?
-
모두 감사 1
덕분에 저녁 빠르게 고름 참고로 메뉴는 육회&연어 덮밥
-
현역 때 계속되는 생윤 3~4에 위기감을 느끼고 생윤을 갖다 버린 후에 (아무리...
-
6모 9모 둘다 2등급인 재수생인데 거의 1일1실모중입니다. 근데 22,30번은...
-
고2 정파 11모(10.15) 범위 맞춰서 공부해야할까요 9
고2 정시파이터입니다 수2 뉴런 미분부분 조금이랑 적분 들으면 완강인데 이번 11모...
-
매기기 두렵네 유기할까 ㅋㅋㅋ
-
그 말이 옳을까?
-
메가패스 쓰고있는데요 12월31까지 85일 지나면 종료된다고 뜨는데 이 기간 끝나고...
-
ㅈㄱㄴ 언매 미적 영 사문 지1 이고 내신 cc입니다..
-
대학가서도 못함
-
완강 얼마나 걸리셨나요
-
그냥 수능 공부 하던대로 하나요?
-
최저용으로 3컷만 맞으면 되는 상황인데 엔제나 실모풀어야할까요
-
화상과외인데 미소녀 AI버튜버 방송하는거처럼 미소녀 띄워놓고 목소리도 바꿔서 과외하는거임
-
공부해야되는데 1
네
-
내년 수능 응시하는 군바리입니다(과탐vs사탐)(올해 전역) 2
안녕하세요 올해 전역자인 군바리입니다 지금 현재 상태는 노베인데 목표는 서성한...
-
설맞이 엔제<<<< 2,3따리한테 원래 빡센거맞음? 걍 유기해도 되나?? 진심 반절...
-
이게맞나..






























옆동네 옆옆동네에서 잘 보고 있습니다감사합니다!!
와 쌤 과외 받았던 학생인데,,, 잘 계시나요 ㅠㅠ
감사했습니다!! 덕분에 카이스트 가서 잘 지내고있어요