실생활과 연속함수

Question

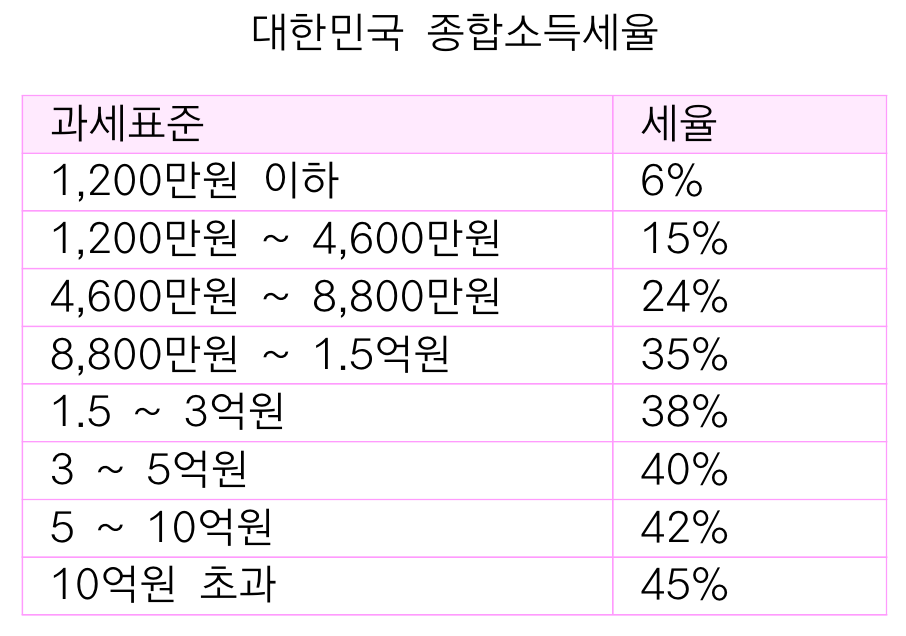
대한민국의 종합소득세율은 위와 같습니다.

아직 수험생분들이라 잘 모르셔서 위의 표를 보고 다음 의문이 생길 것입니다.

1. 돈을 적게 버는 것이 더 좋은 것 아닌가요?

8,900만원 벌어서 세금 35%를 내면 총 57,850,000원을 벌고,

8,700만원 벌어서 세금 24%를 내면 총 66,120,000원을 버는데

돈을 적게 버는 것이 더 좋은 것이 아닌가요?

만약 위의 규칙처럼 세금을 내게 된다면 세금에 대한 대략적인 그래프는 다음과 같이 불연속함수가 나오게 됩니다.

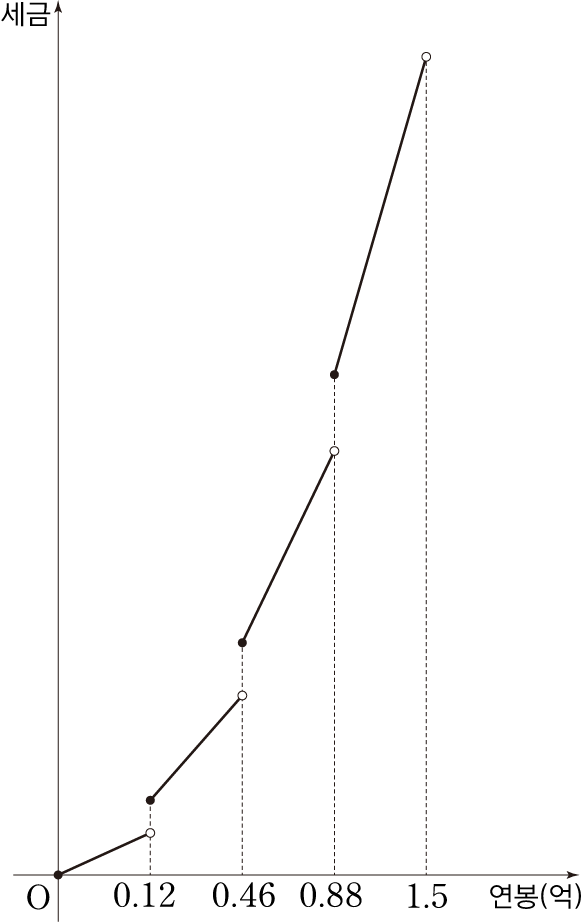
그런데 그렇지 않습니다.

세금제도를 만드는 똑똑한 사람들은 당연히 연속함수를 알고 있고,

그런 모순을 알고 있습니다.

8900만원 버는게 8700만원 버는것보다 더 안 좋게 된다면 사람은 노력하지 않게 되고

자연스럽게 집단도 발전할 수 없게 됩니다.

그런 모순을 막는 것이 제도를 만드는 사람이 해야할 일입니다.

어떤 집단의 노력의 총합은 곧 그 집단의 발전으로 이어지기 때문이지요.

만약 위와 같이 세금제도를 그대로 둔다면

의도적으로 그 집단을 망하게 하고 싶은 누군가의 의지라고 해석해도 무리가 없을 것입니다.

직장으로 비유하면, 일을 더 잘하는 사람이 연봉을 더 많이 받아야 한다는 당연한 말과도 같습니다.

2. 모순을 어떻게 해결하느냐?

결론만 먼저 말하면, 절댓값(일차함수)의 합으로 세금제도를 구성합니다.

l일차함수l는 연속이므로 그들끼리 더하고 뺀 함수도 당연히 연속입니다.

예를 들어, 8,900만원 벌 때

1,200만원까지는 6%를 적용하고,

1,200~4,600만원까지는 15%,

4,600~8,800만원까지는 24%,

8,800~8,900만원까지는 35%를 적용하여 세금을 계산합니다.

1,200X6%=720,000원

(4,600-1,200)X15%=5,100,000원

(8,800-4,600)X24%=10,080,000원

(8,900-8,800)X35%=350,000원

위의 값을 모두 더하면 16,250,000원이 나옵니다.

즉, 8,900만원을 벌면 종합소득세는 약 1600만원이 나오게 되는 것입니다.

(물론 현실에서는 여기에 지방세, 국민연금, 건강보험료 등등등등등등 다른 숨겨진 세금들도 나가서 훨씬 적게받음. 우리는 연속함수가 실생활에서 어떻게 활용되는지 공부하기 위한 것이므로 종합소득세로 이야기를 한정함)

즉, 1에서 공부한 종합소득세 그래프를 구간별로 적절히 평행이동한, 다음 그래프가 실제 종합소득세 그래프입니다.

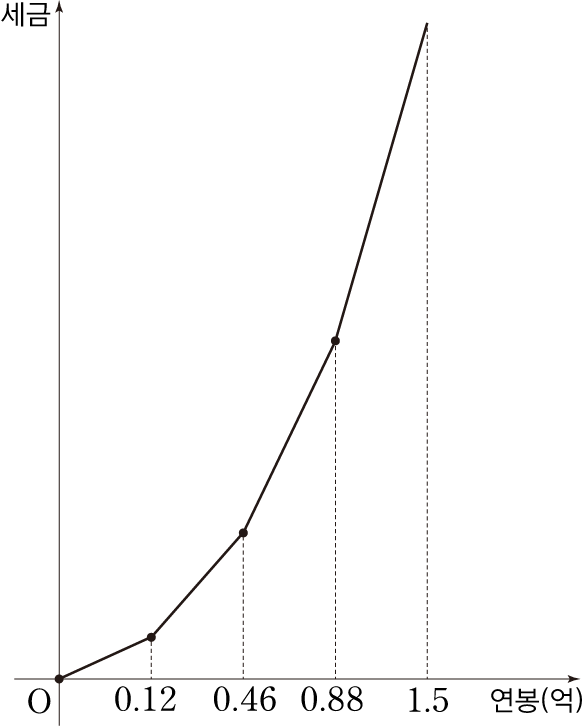
따라서 8700만원버는 사람보다, 8900만원 버는 사람이 더 큰 돈을 벌게 되는 것입니다.

이러한 방식으로

모순이 없도록 제도를 잘 만들어야,

사람들의 행동과 시장에서 모순이 최소화가 되어

세상이 자연스럽게 잘 돌아가는 것입니다.

그래프가 연속이면서 동시에 미분가능에 가까울수록 시각적으로도 가장 자연스러움을 느끼게 되어 있습니다.

거기에 이계도함수까지 존재한다면 금상첨화로 그래프에 아름다움이 생깁니다.

이런 것을 보면 제도를 만드는 사람은 확실히 적어도 연속함수를 알 정도로는 똑똑해야 하는 것 같습니다.

3. 연속함수도 잘 모르는 사람이 대다수일텐데, 세금 계산을 어떻게 쉽게 하나?

그래서 세무사라는 전문가가 존재하여 대리로 맡겨도 되지만,

일반인도 쉽게 계산할 수 있도록 '누진공제액 = 수학적으로 그냥 적절한 평행이동량'을 제공합니다.

이를 누진공제액이라 부릅니다.

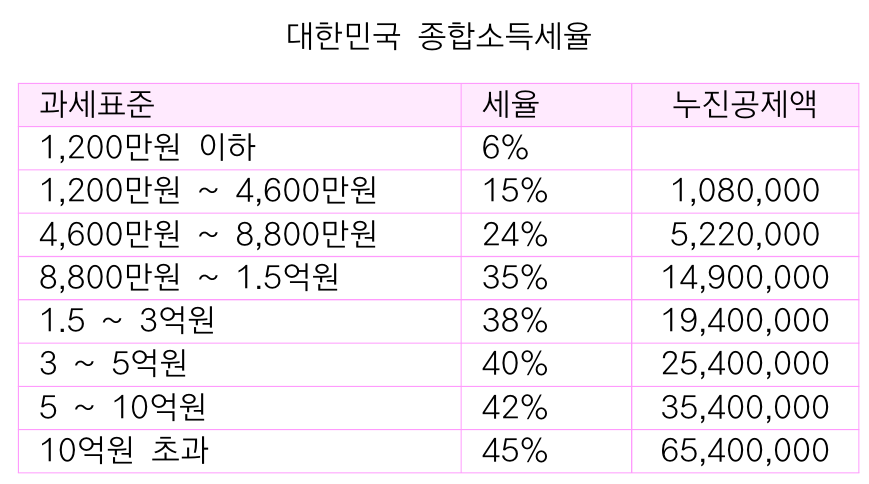
예를 들어, 8,900만원을 벌면 다음과 같이 편하게 계산하면 됩니다.

(8,900)X(해당구간의 세율 35%) - (누진공제액 14,900,000) = 16,250,000원

이 금액은 위에서 복잡하게 계산한 세금과 같음을 확인할 수 있습니다.

여기까지 잘 따라왔다면

역시 수학을 알아야 세상을 이해하는데 도움이 된다는 것을 알 수 있고,

적어도 제도를 만드는 사람은 수학을 어느 정도 알아야 한다는 것도 알 수 있습니다.

4. 다른 예시도 보여주세요.

다른 세금도 보겠습니다.

상속세율입니다.

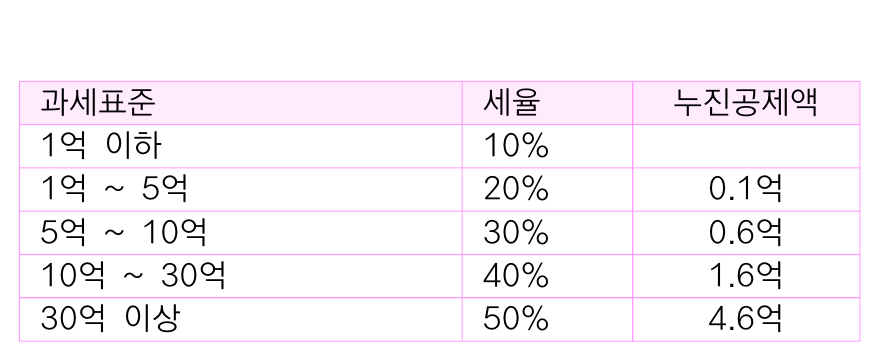
4억 9999만원을 상속하는 사람이

5억 1만원을 상속하는 사람보다 이득을 볼 수 없도록

연속함수로 구성하였습니다.

역시 상속세율을 만든 사람도 연속함수를 알고 있는 것 같습니다.

상속세율에서도 이 세상을 왜곡하지 않기 위해 노력하는 '제도를 만드는 사람'을 엿볼 수 있지요.

이번엔 2021년 현재 아파트 매매시 대출기준을 보겠습니다.

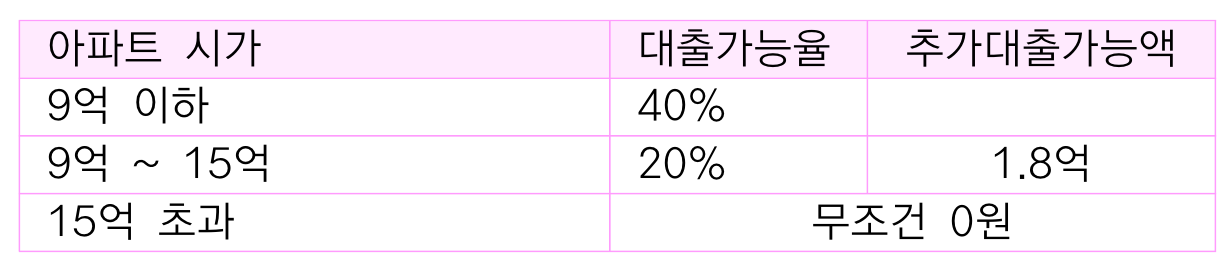
14억 9999만원 하는 아파트를 사면 4억 8천 대출이 나오고

15억 1만원 하는 아파트를 사면 0원 대출이 나오는 시장왜곡이 개오질것같은 기적이 일어났습니다.

제도를 만드는 사람의 두뇌에 대한 믿음이 사라지는 순간이지요.

혹시 연속함수, 미분가능성에 대하여 잘 모르는 문과가 만든거 아닐까요???

(농담임 ㅈㅅ 요즘 문과분들은 연속함수 잘 아시죠 ㅎㅎ)

원본 저장하기

[출처] 실생활과 연속함수 (포만한 수학 연구소) | 작성자 난만한

실수로 오후 6시에 일어난 김동욱 · Accepted Answer

"경제"를 선택했다면 너무나도 익숙한 것

ㅇ빌런 · Answer

상속세 ㅇㅁ 뒤졌네 ㅅㅂ

Evolved Slave II · Answer

와! 재밌는 경제지식!

뀨우꾸웅 · Answer

너무 떼간다 진짜

sincerly · Answer

뭔가 라끌옹님이 쓰신 느낌이 약깐

실생활과 연속함수

최근 게시글 · 더보기

공부를 도와주는 학습자료