안녕하세요. 이원엽입니다.

오늘은 병리학을 공부하고 있습니다.

내일부터 시험기간이에요. 하지만 여러분도 시험기간이지.

화이팅 하시길 바랍니다. 제가 배운 경험을 여러분께 전달할 수 있도록 노력하겠습니다.

예전 2015년쯤에 올린 글을 정리해서 재업합니다.

저는 기말고사를 무사히 끝내고 어떻게든 찾아뵐 수 있도록 노력할게요..

제가 많이 받는 질문은 

수능에 필요한 개념만 압축해서 배우면 안되나?

하는 질문입니다.

네. 문제를 푸는 것은 가능하겠지요. 그러나 수능을 잘 볼 수는 없습니다.

개념이 어디에 쓰이는 지를 이해하고 적용할 수 있어야합니다.

상위권 학생들의 말을 들어보면 수능문제 풀이는 아이디어와 발상이 필요하다 합니다.

그렇다면 그 발상과 아이디어는 어디서 나올까요?

간단한 교과서의 개념에서 나옵니다.

왜 문제를 이렇게 풀어야하지? 왜 이게 제일 좋은 풀이일까?

이 질문에 교과서는 최대한 쉽고 명확하게 제시해주고 있습니다.

하지만 대부분의 학생들은 인강 교재나 학원 부교재를 보면서 그것이 개념의 끝이라 생각합니다.

그 교재에는 이런저런 잡다한 문제풀이방법, 스킬들이 있을겁니다. 아무것도 모르고 그것을 외우죠.

그러면서 수학은 외우는 과목이라며, 머리가 좋은 애들이 잘하는 과목이라고 생각해버립니다.

그렇지 않다구요.

왜 분자에 유리화를 해야할까?

다음 예제를 풀어봅시다.

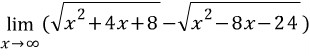
이 문제를 풀지 못하는 학생은 거의 없을겁니다.

당연히 시중문제집에서는 이런 문제의 풀이를 적어놓았거든요.

유리화를 해서 극한을 구해라 라고 하지요.

우리는 분모에 유리화를 하는 건 배웠어요. 분모에 무리식이 있으면 계산이 힘들다는 이유로 말이죠.

근데 왜 이 계산을 할 때는 분자에 유리화 해야할까요??

이것을 이해하면서 문제를 풀고 있나요?

함수의 극한값의 계산성질

교과서에 나와있는 개념중에는 다음과 같은 성질이 있습니다.

혹시 이 개념을 깊이 생각해본 적 있으신가요?

함수값이 존재한다는 것은 수렴한다는 이야기입니다.

즉, 극한의 계산은 수렴할 때만 계산할 수 있다는 얘기입니다.

위의 함수는 수렴하지 않아요. 그래서 극한값을 계산할 수 없습니다.

그렇다면 어떻게 해야할까요? 수렴하는 함수로 모양을 바꾸어주어야 합니다.

근데 이 결과도 수렴하는 함수의 극한이 아닙니다.

12x는 x가 무한대로 가면 발산하구요, 분모도 무한대로 커지면 발산하죠.

그렇다면 어떻게 해야할까요?

유리식의 성질 중 분모와 분자를 0이 아닌 같은 수로 나누어도 성립한다고 합니다.

그렇다면 식에서 같은 수 x로 나누어 줄 수 있겠죠

그래서 다음과 같이 변형됩니다.

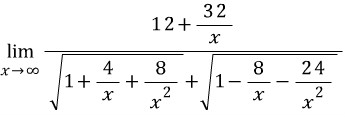
x가 무한대로 갈 때 12+32/x는 12로 수렴합니다.

분모에 있는 함수도 x가 무한대로 갈 때 2로 수렴하므로 답은 6이 됩니다.

이제 저런 꼴의 극한에서 유리화를 왜 시켜주어야 하는가에 대한 답으로,

수렴하는 함수의 꼴로 만들어주기 위해서! 라고 하시면 됩니다.

그래야 계산이 되니까요.

극한값의 계산 단원은 공부를 하지 않고 넘어가는 학생들이 많습니다.

문제가 쉽게 출제되기 때문입니다. 최고차항의 계수 비교하고 유리화 외우면 되니까요..

하지만, 그렇게 하시면 안된다는 겁니다.

수렴할 때에만 극한값을 구할 수 있다는 것을 이해하셔야 이해할 수 있습니다.

평가원 기출문항 풀이

다음 예제를 풀어보세요.

(2006년 6월 평가원 기출문제, 출처는 평가원 기출문제 자료실입니다.)

이 문제를 어떤 식으로 접근해야할까요? 생각해봅시다.

(나)의 극한값이 존재한다고 하였습니다. 즉 수렴한다는 것이죠.

그렇다면 극한값을 계산해서 풀어야하는데, 분모에 X에 0을 대입하면 0이 되어버립니다.

이 법칙중 4번에서 g(x)와 베타가 0이면 계산할 수 없다네요.. 어떻게 해야할까요?

이것을 파악한다면 우리의 목표는 명확합니다.

분모가 0이 되지 않도록 식을 변형해볼 방법이 없을까?

어떻게 변형할 수 있을까요?

분모와 분자에 같은 수를 나누면 식이 성립합니다. 

그렇다면 x로 나누어보면 되지 않을까요?

적어도 분모에 k는 남으니까, k는 수렴할겁니다. (f(x)/x=-k일 때를 제외해야하지만, 왠만해서는 괜찮을거에요!)

그 나머지가 수렴하는지만 생각해보면 되지 않을까요?

x로 나누어보면 정확하게 그 나머지가 x=0일때의 미분계수, 

즉 fi'(0)으로 수렴하게 되며

수렴하는 함수에 대한 극한값의 계산에 의해서 극한값을 계산할 수 있게 됩니다.

이 문제는 꽤 쉬운 문제입니다. 한번 풀면 확실하게 이해가 되는 문제죠.

중요한 것은 이 문제에 접근하는 아이디어가 어디에서 나왔냐는 겁니다.

그 아이디어는 너무 간단해서 눈여겨 보지 않았던 극한값의 계산에서 나왔습니다.

교과서의 개념이 간단해도 깊이 생각해보고 따져봐야합니다.

문제 풀이를 위한 개념공부가 아닌 개념을 쌓아가는 데에 초점을 두는 공부를 하셔야합니다.

시간이 되면 6월 모의고사에 대한 마음가짐도 올리고싶지만

아마도.. 공부해야할 것 같습니다. 최대한 올리는 방향으로 할게요.

P.S. 1) 바쁩니다. 혹시 제게 질문이 있다면, 쪽지 혹은 제 페이지, 혹은 제 개인 연락처(?)

로 보내주시면 어떻게든 최대한 답변드리겠습니다. 지금 1주일 뒤면 더 그럴겁니다. 기말고사라서요..

후 살고싶습니다. 살고싶어요. 살려주세요.

P.S. 2) 혹시라도 형편이 어려운 학생이 있다면, 언제든 연락주시길 바랍니다.

비록 학생의 신분으로 많은 지원은 어렵습니다. 

정말 정말 정말 조금만 도움을 드릴겁니다. 하지만 제가 낭비하는 시간을 모두 모을수는 있습니다.

어렵습니다. 제가 직업을 가진 사람이었다면, 기꺼이 모든 이들에게 좀 더 나은 지원을 해드리겠으나

그렇지 않은점은 제가 모자라기 때문입니다. 미안합니다. 아주 작은 도움이겠으나 최대한 돕겠습니다.