돌림힘 분산법 대표적인 질문
게시글 주소: https://orbi.kr/00012224657
Q : "받침점이 3개 이상이면 못쓰나요?"
A : 영향력을 구하는것은 불가능하나 문제 조건을 응용하면 가능합니다.
대표적인게 17수능이지요.
밑에 받침점이 4개라서 안될것같지만 분산법은 "수직항력으로 접근"하는것입니다.
일단 수직항력 F라 하면 4F=2F+4m, F=2m으로 수직항력은 구할 수 있을것입니다.
그 다음이 문제겠죠?
왼쪽에서 두번째 기둥까지의 거리가 궁금한것이죠.
이럴땐 필요한 받침대만 빼고 지운다음 힘으로 나타내주면 됩니다.
한번 1,2,3,4번 받침대중에서 2, 3번 받침대만 지워볼까요?
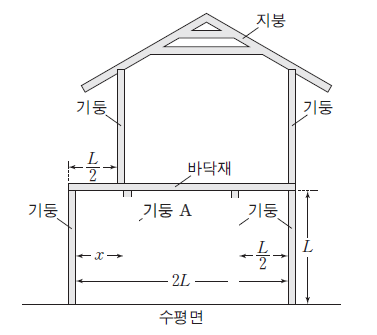
이러면 받침대가 두개고 아래에서 2m의 힘(2,3수직항력)이 위로 작용하고
양쪽 받침대 영향력이 (2m,2m)이라고 하면 되겠습니다.
전체 영향력 = (2m,2m)
왼쪽 기둥+수직항력 = (2.25m, 0.75m)
오른 기둥+수직항력 = (0, 3m)
바닥재 = (m, m)
3번 기둥 = (-0.5m,-1.5m)
따라서 2번기둥 = (-0.75m, -1.25m)
2번기둥으로부터 양쪽 거리비가 5:3인데 합이 2이므로 4씩 나눠주면 x=5/4이 나오게 됩니다.
*분산법은 수직항력으로 접근하는것입니다.
*그와 동시에 수직항력을 힘으로 해석하면 다른 받침대에 대한 영향력이 나오겠습니다.
비슷한 예로 14수능 20번이 있습니다.
이 문제는 받침대가 밑에 하나만 존재합니다.
이럴때도 힘의 방향을 추론하거나 수직항력적으로 해석하면 됩니다.
만약 철수 영희 아래에 받침대가 존재했다면 그 받침대에 작용하는 힘의 비는 3:2가 될것입니다.
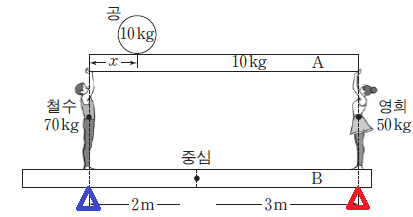
즉, 이때 파란, 빨간 받침대에 대한 영향력의 비는 3:2가 되어야 겠습니다.
따라서
철수영희 = (70,50)
막대A = (5,5)
공= (10-2x,2x)
전체=(85-2x,55+2x)=(3k,2k)=3:2
165+6x=170-4x, x=0.5
임의로 그리고 지우면서 풀이가 간결해지는경우도 상당히 많죠 :)
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
(4x-y)(4y-x)=30^6. x,y자연수(x,y)의 개수는?
-
확통사탐 기준 노베로 어디까지 가능할까
-
풍경이 아름답죠? 가는 길 외롭지 않게 응원해주세요. 하 집까지 겁나 머네 진짜
-
x^4-2y^2=1x,y 정수해 2개
-
무덤 속의 벙어리를 말한 셈이다
-
sqrt(x)+sqrt(y)=sqrt(z)자연수, x,y,z 해 무한개임
-
일단 정년 연장하는데 청년 일자리가 어떻게 늘어나냐 하니까 너무 극단적이라고...
-
보통어느정도 푸시나용
-
[자료] 공통+확/미/기 전범위 수학 실모 하나 뿌림 6
예에엣날에 만든 문제들 짜깊기해서 만든 문제라서 요즘 트랜드에 맞지 않을 가능성이...
-
부정방정식 풀어보실 15
m^n=n^(m-n)m,n은 자연수
-
x!+y!=x^yx,y는 자연수
-
심심함
-
n*2^(n+1)+1=k^2.n,k 는 자연수
-
지방러라 울었다 9
서울 근처 안살아서 서울 한 번 가는데만 시간과 돈이 얼마나 깨지는거야 고생은 덤이고 에휴
-
축하해드림
-
차단률이 감소한다고한다 --
-
자야지
-
필기 안해봄 4
도전해봣는데 끔찍해서 관둠
-
ㅈ같다 벌써
-
왜 다 어디서 본 문제들이지
-
제 선택과목 3
물화생지
-
국어를 잘해져서 1
훈수두고 싶다
-
폰이 너무너무 무거워짐
-
진도율 5퍼 7
사실 한 3번 들어서 305퍼임
-
본인 37점인데 백분위 90 2등급뜸
-
어라?
-
자고 싶다 0
영~원히
-
정시 관련 질문 3
정시 생각중인 고2인데요ㅠㅠ 아는게 없어서 질문 많이 달아요 아는거 아무거나...
-
난 다 들었는데 0
진도율 보정을 어케했길래 이지랄 남 다른 강의들도 진도가 반토막남
-
어디든 좋으니 나와 가줄래
-
국어 문학은 수특 문제 풀고 ebs 인강 듣고 있고 비문학은 혼자 글을 이해하는게...
-
학습은 뇌가 알아서 해주겟지 해줘 그냥
-
3단원 끝남 6
사실 끝낫다는게 개념만 쭉 들엇음 사실 그마저도 1강 남앗음 4단원 강의 개 많음 종합적으로 귀찮
-
오노추 2
-
고등학교만 10년 다닐뻔함 수업 몇시수 들었는지 체크해서 시수 모자르면 미이수 된다던데
-
일단 수학은 원래 수1 수2 알텍 3회독 하면서 기출 2회독 정도하고 미적은 생질,...
-
회차별로 0~2개정도 틀리는것같은데 이제 뭐해야할까요? 사규는 이미 배송시킴
-
6모 생명은 6
샤가프랑 복제추론, 코돈, 뭐지?이렇게 4개인가 근데 개념형도 못 풀꺼 같은데 음..
-
생각하지 못한 반전과 친구들과 일탈과 누려보지 못한 성인+자유는 극락이라고 생각함...
-
서울갓반 과중고 2점대인데 이 점수로 목표대학은 어려울 거 같아 정시 파이터가...
-
너와 마신 커피 한 잔에도 난 세상을 가졌어
-
일어나보니 4
너가 없더라
-
뭐 왓츄세이
-
송도가 유배지면 2
여긴 뭘까
-
오르비 잘자 6
-
만약에 간다고 하면 사문이 낫나요 아니면 생윤이 낫나요?
-
그냥 순수하게 행사가 많음 학교 행사들.... 특히 기숙사 rc활동요 송도가...
-
개졸려요 ㅁㅊ 하긴 오전 6시부터 자정까지 대구 -> 인천 -> 대구 이러고...
-
고3가서도 비슷하게 나옴? 거의 99 실수 좀 하면 98



















































엇 좋은글!ㅎㅎ