"Chapter. 0 - 등차수열의 합"
게시글 주소: https://orbi.kr/00072252175
“Chapter. 0 – 등차수열의 합”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “등차수열의 합”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
등차수열은 앞 “등차수열”칼럼에서 설명 드린것과 같이 이미 잘 알려진 함수이기에 출제하기 까다로운 부분이 많습니다.
특히 등차수열임을 직접알려주지 않고 그 합으로써의 표현을 통해 등차수열을 알려주는 문제들이
가장 많이 출제가 되는 동시에 학생들이 많이 틀리는 대표 문항 중에 하나입니다.
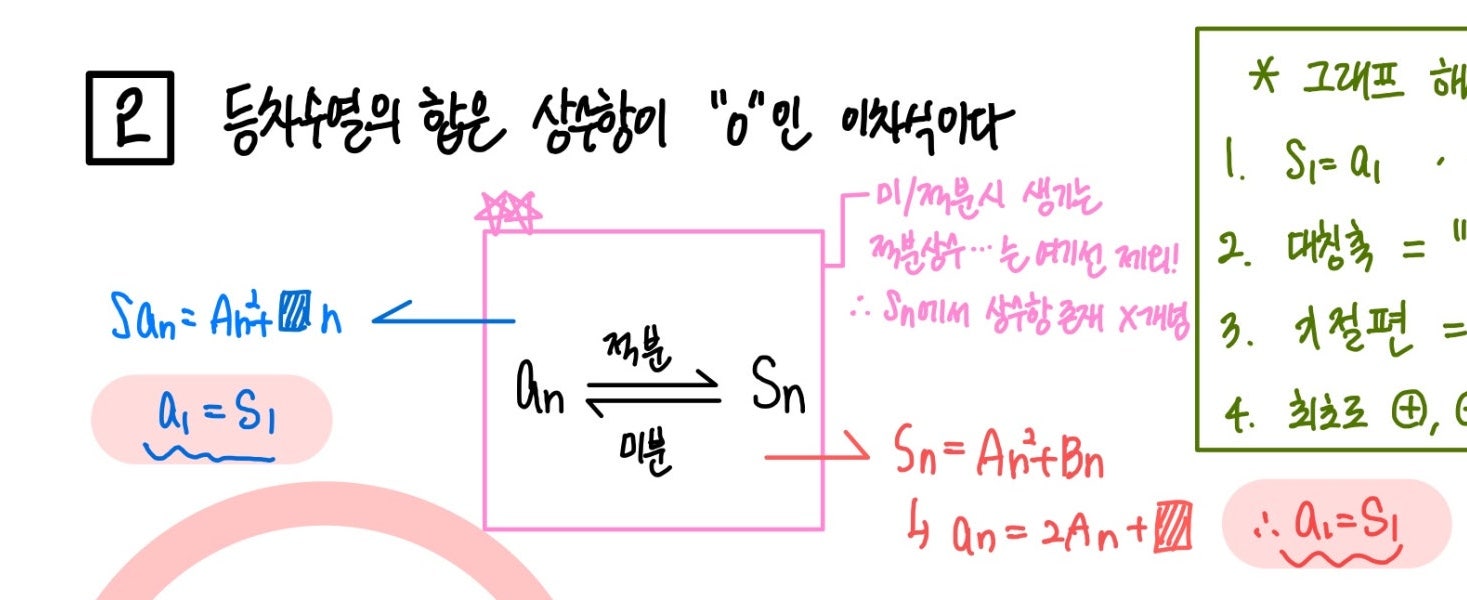
등차수열의 합에 대한 일반항과의 관계입니다.
등차수열의 합의 일반항은 ‘d/2n^2+an’입니다. 이는 시그마를 이용해여 증명이 쉽게 가능합니다.
이를 이용하여 우리는 등차수열의 합과 일반항 사이에 독특한 관계를 찾을 수 있습니다.
바로 서로 미적의 관계를 갖고 있음을 알 수 있습니다. 이것은 시그마의 계산을 통해 등차수열의 관계에서 서로
미적의 관계를 갖고 있는 것입니다.(완벽한 미적의 관계가 아닌 최고차항을 중심으로 한 미분의 개념)
그리고 이때는 최고차항의 계수만을 사용합니다!! 상수항은 따로 우리가 직접 구해야합니다!
이해하기 쉽게 사진과 함께 살펴봅시다. 등차수열의 합을 미분하면 최고차항인 n에 대한 계수를 취하고
그 나머지 상수항은 ‘S(1)=a(1)’임을 사용하여 알아내야 합니다!
이는 복잡하거나 찾기 어려운 식에서 등차수열의 일반항을 바로 찾을 수 있다는 장점을 가지고있습니다.
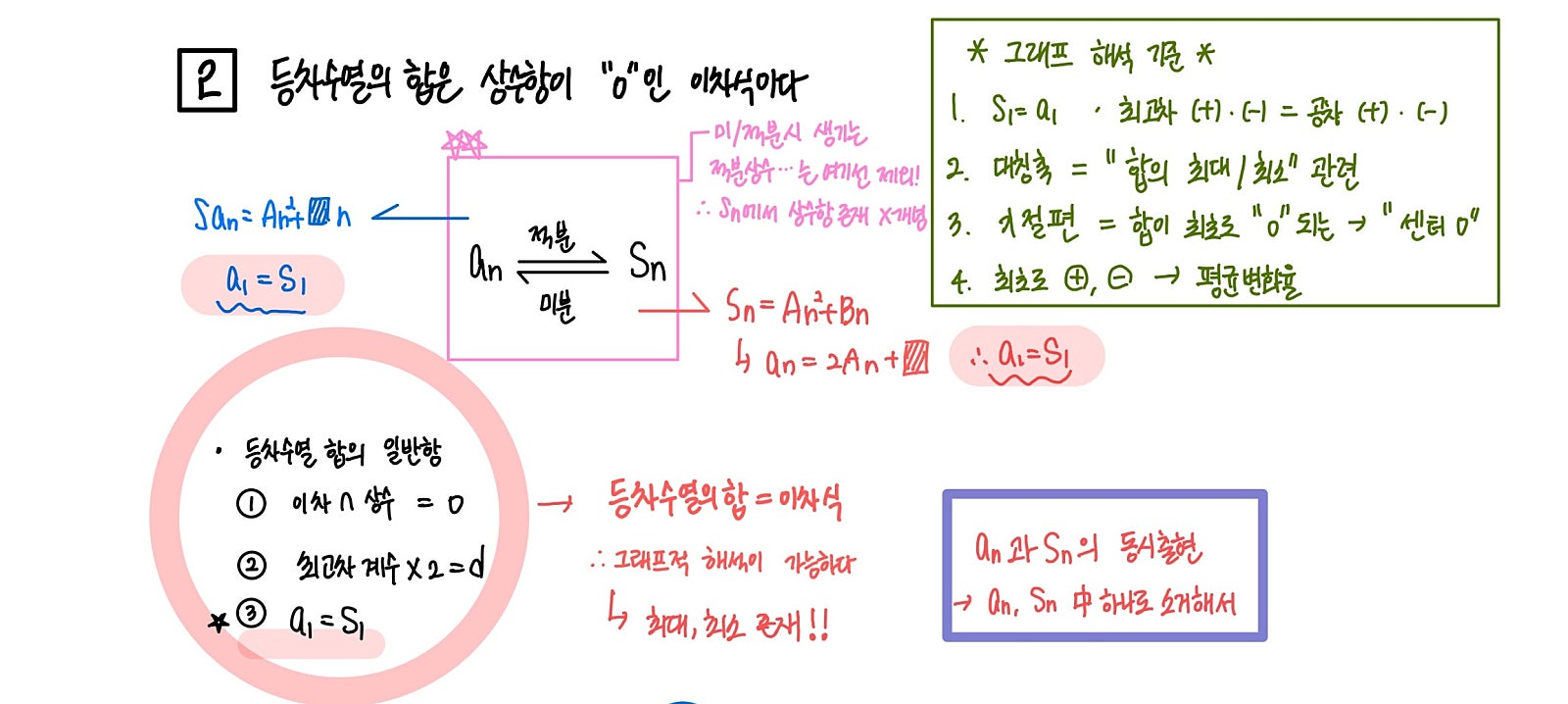
상수항을 직접 꼭 구하자!
등차수열의 합은 상수항이 “0”인 이차식이기에 만일 복잡한 알 수 없는 수열의 합이
상수항이 0인 이차식이라면 바로 그 수열이 등차수열꼴 임을 확인할 수 있습니다. 그리고 그 합의 식을 미분하여
등차수열의 일반항까지 바로 구할 수 있습니다!
다만 여기서 중요할 점은, 일반항을 적분하게 되면 적분상수가 붙지만 우리는 적분상수는 고려하지 않는 다는 점입니다.
그 이유는 수열의 단원에서 미적분의 개념을 빌려 사용하는 것이기에(시그마의 원리를 적용하여)
적분상수는 따로 추가하지 않고 계산합니다!!
또한 이렇게 적분상수는 고려하지 않기에 우리는 등차수열의 합에서 일반항을 구할 때 미분 한뒤
그 첫째항은 직접 대입해보아 구해야합니다.
-> 앞에서 설명한 S(1)=a(1)
예를 들어서 알아봅시다.
Q. 모든 n에 대해 식을 만족하는 어떤 수열의 합 Sn= 3n^2 + 7n일 때 이 수열의 5번째 항을 구하여라.
-> 먼저 수열의 합이 상수항이 0인 이차식이니 이 수열의 일반항은 등차수열의 꼴임을 알 수 있습니다. 따라서 위 식을 미분한 ‘6n + 7’에서 최고차항인 6만 취하고 나머지는 S(1)=a(1)을 통해 구해봅시다!
a(n)=6n + ?이니 S(1)=3 + 7= 10, 따라서 a(1)= 6 + ?= 10이므로
a(n)=6n+4임을 알 수 있습니다.(단 이때, n존재하지 않는 이미지입니다.2)
그리고 구하는 항은 5번째의 항이니 n에 5를 대입하여 34임을 쉽게 알 수 있습니다.
우리가 이 개념을 알지 못했을 땐 이 문제를 풀기 위해 ‘S(n)-S(n-1)’를 계산해야 하는데 이렇게 되면 계산이 정말 극도로 복잡해집니다. 안 그래도 2차식인데 이를 계산하려함은 시간이 많이 들겠죠..
이렇게 등차수열의 합과 그 일반항의 관계에 대해 알아보았습니다.
하지만 제가 등차수열 첫 칼럼에서 강조한 부분을 다시 보시면!
수열을 단순히 수의 나열로 바라보는 것이 아닌 함수로써의 해석이 가능하다고 했습니다.
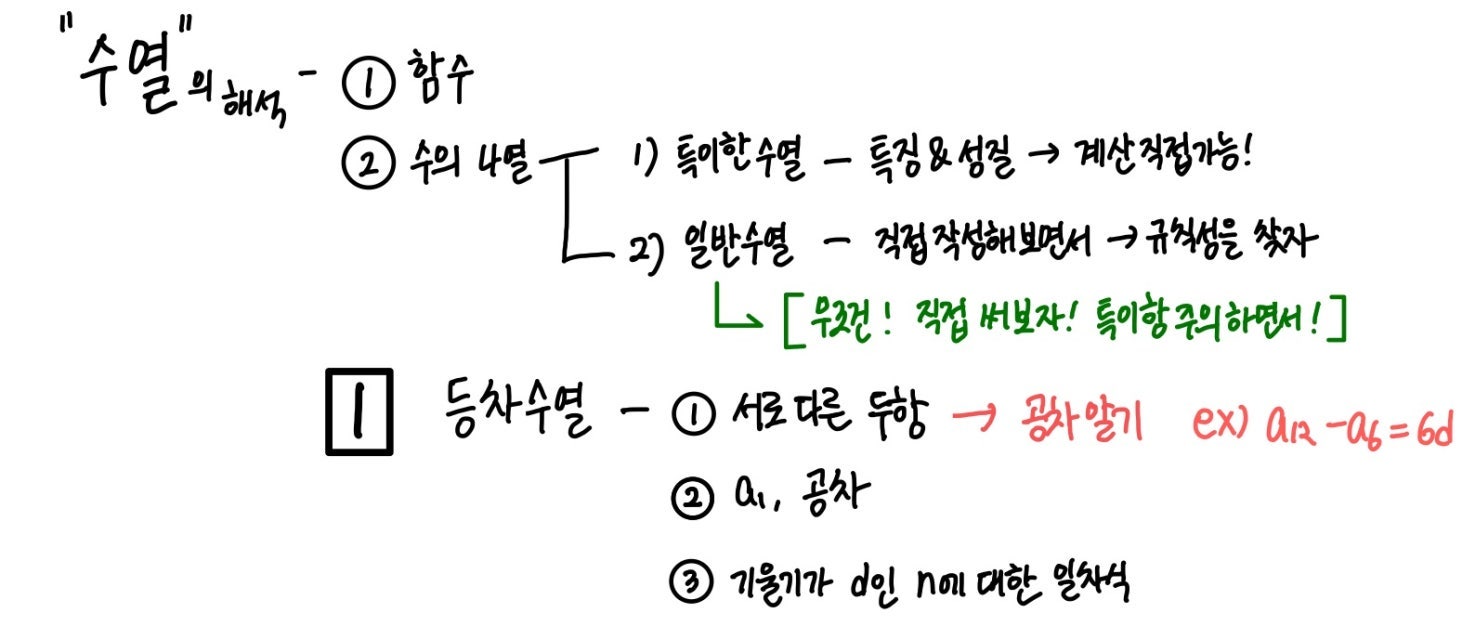
함수로써의 해석이 가능하도록 생각해야합니다.
등차수열의 합은 상수항이“0”인 이차식입니다. 이 사실을 이용하면 우리는 등차수열의 합이 무조건 “0”을 근으로 갖는 이차함수로써의 해석이 가능하다는 것을 알 수 있습니다. 특히, 문제를 보면 수열의 합이 최대가 되는 지점/수열의 합이 처음으로 음수, 양수가 되는 지점을 물어보는 경우가 많습니다.
이럴 때 따로 계산을해서 직접 그 항을 구하지 말구 우리는 최대가 되는 지점 = 이차함수의 꼭짓점/ 수열의 합이 처음으로 음수, 양수가 되는 지점 = 이차함수의 해(0이아닌 해)임을 사용하면 귀찮고 복잡한 계산 없이 쉽게 구할 수 있습니다!
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
https://cafe.naver.com/suhui/28780393
자료의 원본 자료는 여기서 확인하실 수 있습니다!
자료 구매나 후기는 댓글이나 들어오셔서 톡으로 연락 주시면 자료안내 도와드리겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
호오오님 프사 2
-
똥냄새 안나쥬?ㅋ
-
담주에도 이 재미없는 똑같은 루틴이라니... 나도 부라 오자마자 상쾌한 마음으로...
-
[자작문제] 수2입니다 18
참고** 어떤 사설. 기출 문제도 참고하지 않았으며 100% 본인 발상으로 만든...
-
근데 또 켜기는 귀찮음
-
일단 전 아님
-
왜냐면 이제부터 기다림이 24시간이 넘을 때마다대가리를 존나 쎄게 쳐서 제 머릿속을...
-
올해 뉴런 수1 기준으로 본책에 있는 문제들 정도 난이도를 쭉 풀어보고 싶은데...
-
근데 20대 남자들 보고 귀엽다하는 나도 또라인듯 16
애니프사단 거의다 뱃지 하나씩은 달고 다니시던데 ㄷㄷ
-
진짜임?? ㄷㄷ;; 뭐 얼마나 어려웠길래...
-
아이디어 하고 기출코드 하는거 별로에요? 기현쌤 좋은데 기코 들어보고싶ㅇㅓ서… 걍...
-
상상 창작 재구성도 예술임
-
물2 시발 고인물들 돌림힘 2차원 운동 눈풀조지고 이상한 풀이로 한줄컷하는 거 보고...
-
무슨 사수생이 그런 의지도 없냐고 막 그러네..폰은 집에 두고 다니긴 했는데...
-
따라하고 싶은데 그 바이브가 안살아 ㄹㅇ
-
22211이면 서성한 경영 되나요?
-
진짜 재미없네
-
고려대 응원가가 진짜 개지린다는게 느껴지네
-
김기현 아이디어 0
쎈 풀고 들어도 되나요??
-
오늘 그린거 인증 12
-
오늘은 사진을 못찍었네요 미적분만 주구장창함
-
다른 뛰어난 분들에 비해선 미천한지라... 그래도 볼만은 한가요..?
-
커리 컴팩트하게 가려고 신경쓰신게 보이고 늦게 런칭한만큼 독서 위주로 투자하신게...
-
외대여서 경영이 디메리트 받거나 그런건 없나요?
-
장례식 가야됨? 참고로 장례식 참석하면 일주일정도 공부 못한다
-
하체가 발달한 편 앵간한 운동은 다 싫어했는데 걷는건 좋아하기도 했고 아버지 쪽이...
-
평균적으로 풀이시간이 평벡>>이차>=공도임
-
이게 설의인가 7
멀엇네
-
선착2
-
밥부터 먹자 2
배고파 진짜 죽겟다 오늘 0끼임
-
강평들은 좀 분발하도록
-
* 자세한 문의는 아래의 링크를 통해 연락 바랍니다....
-
전 좃도 없는데 이거 하나로 어케어케 비벼서 대학가긴함 다만 귀찮음 이슈로 안 쓸 가능성 99퍼
-
넘 아깝다... 난 최선을 다해서 먹었는데 엄마가 항상 많이 보내줌
-
플래너 주문함 2
-
노베들한테 이거 할 시간에 기출 하라는 사람 많네
-
고트와 나란히 있다..
-
https://m.site.naver.com/1Abu2
-
섹준완 ㅋㅋㅋㅋㅋ 10
이게섹스가아니면머임?(진짜모름)
-
1학년때 7등급, 2학년때는 1컷~높은 2등급, 3학년때는 모평 2, 수능 4...
-
문제가 참 볼 건 없는데 풀긴 막막해 보임 실제 수능에 나오면 241122 비슷하게...
-
저는 수학 감 돌아오게 하려고 적당한 준킬러 풀 생각이었는데 240628부터...
-
어나클 같은거 없나요?
-
난 패드도 아니고 노트에 그렸는데 세상 좋아졌다
-
나중에 수학과외하려면 내신확통1등급 찍혀있는 게 나아서? 이런 이유도 있나요?
-
뭐야 물2 재밌네 12
돌림힘 재밌는데?




















































너무 늦게 자료를 올려드려 죄송합니다! 앞으로 더 자주 빨리 올려드릴 수 있도록 노력하겠습니다!